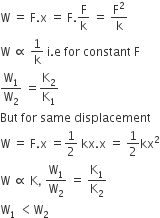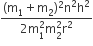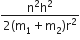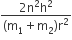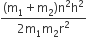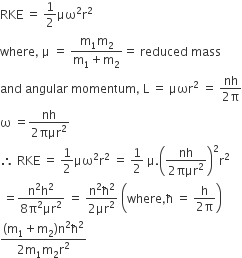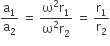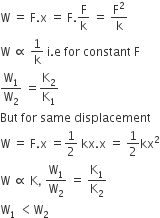A spectrometer gives the following reading when used to measure the angle of a prism.
Main scale reading: 58.5 degree
Vernier scale reading: 09 divisions
Given that 1 division on the main scale corresponds to 0.5 degree. Total divisions on the vernier scale is 30 and match with 29 divisions of the main scale. The angle of the prism from the above data

• 58.59 degree

• 58.77 degree

• 58.65 degree

• 59 degree

A diatomic molecule is made of two masses m₁ and m₂ which are separated by a distance r. If we calculate its rotational energy by applying Bohr's rule of angular momentum quantization, its energy will be given by (n is an integer)

• 
• 
• 
• 

D.

Rotational kinetic energy of the two body system rotating about their centre of mass is

A cylindrical tube, open at both ends, has a fundamental frequency, f, in the air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air-column is now

• m₁r₁:m₂r₂

• m₁ :m₂

• r₁ :r₂

• 1:1

This question has statement 1 and statement 2. Of the four choices given after the statements, choose the one that best describes the two statements.
If two springs S₁ and S₂ of force constants k₁ and k₂, respectively, are stretched by the same force, it is found that more work is done on spring S₁ than on spring S₂.

Statement 1: If stretched by the same amount, work done on S1, will be more than that on S₂
Statement 2 : k₁ < k₂

• Statement 1 is false, Statement 2 is true

• Statement 1 is true, Statement 2 is false

• Statement 1 is true, Statement 2 is the correct explanation for statement 1

• Statement 1 is true, Statement 2 is true, Statement 2 is not the correct explanation for statement 1.

A thin liquid film formed between a U-shaped wire and a light slider supports a weight of 1.5 x10^–2N (see figure). The length of the slider is 30 cm and its weight negligible. The surface tension of the liquid film is

• 0.0125 Nm^-1

• 0.1 Nm^-1

• 0.05 Nm^-1

• 0.025 Nm^-1

D.

0.025 Nm^-1

The force of surface tension acting on the slider balances the force due to the weight.

⇒F = 2Tl = w
⇒2T(0.3) = 1.5 x 10^–2
⇒T = 2.5 x 10^–2 N/m