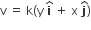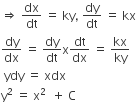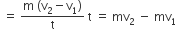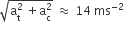+91-8076753736 [email protected]
logo
logo

JEE physics

Sponsor Area

Question
CBSEENPH11020326
Wired Faculty App

STATEMENT – 1
Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.
STATEMENT – 2
Principle of conservation of momentum holds true for all kinds of collisions.

  • The statement I is True, Statement II is False.

  • The statement I is True, Statement II is True; Statement II is a correct explanation for Statement I.

  • The statement I is True, Statement II is True; Statement II is not the correct explanation for Statement I.

  • Statement I is False, Statement II is

Solution

B.

The statement I is True, Statement II is True; Statement II is a correct explanation for Statement I.

Sponsor Area

Question
CBSEENPH12039451
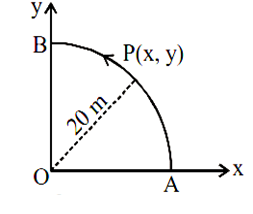
Wired Faculty App

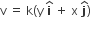A particle is moving with velocity,straight v space equals space straight k left parenthesis straight y space bold i with hat on top space plus space straight x space bold j with hat on top right parenthesis where K is a constant. The general equation for its path is

  • y = x2 + constant

  • y2 =  x + constant

  • xy = constant

  • y2 = x2 + constant

Solution

D.

y2 = x2 + constant

The velocity of the particle,straight v space equals space straight k left parenthesis straight y space bold i with hat on top space plus space straight x space bold j with hat on top right parenthesis 
rightwards double arrow space dx over dt space equals space ky comma space dy over dt space equals space kx dy over dx space equals space dy over dt straight x dt over dx space equals space kx over ky space ydy space equals space xdx straight y squared space equals space straight x squared space space plus space straight C

Question
CBSEENPH11020328
Wired Faculty App

The figure shows the position –time (x – t) graph of one–dimensional motion of a body of mass 0.4 kg. The magnitude of each impulse is

  • 0.4 (Ns)

  • 0.8 Ns

  • 1.6 Ns

  • 0.2 Ns

Solution

B.

0.8 Ns

From the graph it is a straight line, so uniform motion. Because of impulse direction of velocity changes as can be seen from the slope of the graph.
(∴ impulse (l) = f x t
⇒ I  = mat
 space equals space fraction numerator straight m space left parenthesis straight v subscript 2 minus straight v subscript 1 right parenthesis over denominator straight t end fraction space straight t space equals space mv subscript 2 space minus space mv subscript 1
Initial velocity, v1 = 2/2 = 1 ms-1
Final velocity v2 = 2/2 = - 1 ms-1
pi  = mv1 = 0.4 N-s
pf  = mv2 = -0.4 N-s
J = pf-pi = -0.4-0.4
 = - 0.8 N-s
|J| = 0.8 N-s

Question
CBSEENPH11020330
Wired Faculty App

The respective number of significant figures for the numbers 23.023, 0.0003 and 2.1 × 10–3 are

  • 5,1,2

  • 5,1,5

  • 5,5,2

  • 4,4,2

Solution

A.

5,1,2

Question
CBSEENPH11020333
Wired Faculty App

A point p moves in counter -clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out the length s = t3 + 5, where s is metre and t is in second. The radius of the path is 20 m. The acceleration of P when t =2 s is nearly

  • 13 ms-2

  • 12 ms-2

  • 7.2 ms-2

  • 14 ms-2

Solution

D.

14 ms-2

Given that, s  =t3 +5
therefore speed v, = ds/st = 3t2
and rate of change of speed, at = dv/dt = 6t
∴ Tangential acceleration at t =2s
at = 6 x 2  = 12 ms-1
and at t = 2s, v = 3 (2)2 = 12 ms-1
∴ Centripetal acceleration, ac = v2/R = 144/20 ms-2
∴ Net acceleration  = square root of straight a subscript straight t superscript 2 space plus straight a subscript straight c superscript 2 end root space almost equal to space 14 space ms to the power of negative 2 end exponent

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation