The velocity of a particle is v = v0 + gt + ft2. If its position is x = 0 at t = 0, then its displacement after unit time (t = 1) is
-
v0 + 2g + 3f
-
v0 + g/2 + f/3
-
v0 + g + f
-
v0 + g/2 + f
B.
v0 + g/2 + f/3
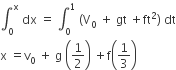
Sponsor Area
The velocity of a particle is v = v0 + gt + ft2. If its position is x = 0 at t = 0, then its displacement after unit time (t = 1) is
v0 + 2g + 3f
v0 + g/2 + f/3
v0 + g + f
v0 + g/2 + f
B.
v0 + g/2 + f/3
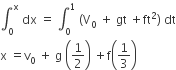
Sponsor Area
A block of mass ‘m’ is connected to another block of mass ‘M’ by a spring (mass less) of spring constant ‘k’. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is stretched. Then a constant force ‘F’ starts acting on the block of mass ‘M’ to pull it. Find the force on the block of mass ‘m’.
mF/M
(M+m)F/m
mF/(m+ M)
MF (m+M)
C.
mF/(m+ M)
If gE and gm are the accelerations due to gravity on the surfaces of the earth and the moon respectively and if Millikan’s oil drop experiment could be performed on the two surfaces, one will find the ratio (electronic charge on the moon/ electronic charge on the earth) to be
1
0
gE/gM
gM/gE
A.
1
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The centre of mass of the new disc is α/R from the centre of the bigger disc.The value of α is
1/3
1/2
1/6
1/4
A.
1/3
In this question distance of centre of mass of new disc is αR not α/R.

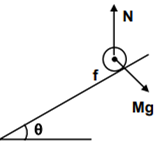
A round uniform body of radius R, mass M and moment of inertia ‘I’, rolls down (without slipping) an inclined plane making an angle θ with the horizontal. Then its acceleration is
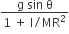
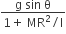
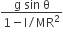
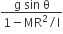
A.
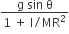
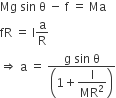
Sponsor Area
Mock Test Series