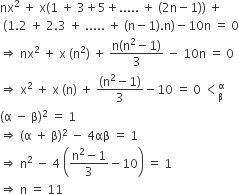
Sponsor Area
If, for a positive integer n, the quadratic equation,
x(x + 1) + (x + 1) (x + 2) + .....
+ (x + n -1 ) (x + n) = 10n
has two consecutive integral solutions, then n is equal to :
11
12
9
10
A.
11
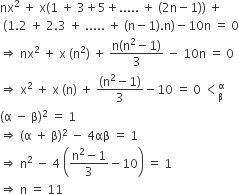
Sponsor Area
The function 
neither injective nor surjective.
invertible
injective but not surjective.
surjective but not injective
D.
surjective but not injective
The following statement
(p → q ) → [(~p → q) → q] is
a fallacy
a tautology
equivalent to ~ p → q
equivalent to p → ~q
B.
a tautology
(p → q) → [(~p → q) →q]
(p → q) → ((p → q) → q)
(p → q) → ((~p → ~q) → q)
(p → q) → ((~p→ q) → (~q→ q))
(p→ q) v (p → q) which is tautology
For any three positive real numbers a, b and c, (25a2 + b2) + 25(c2 – 3ac) = 15b(3a + c), Then
b , c and a are in G.P
b, c and a are in A.P
a, b and c are in A.P
a, b and c are in G.P
B.
b, c and a are in A.P
225a2 + 9b2 + 25c2 – 75ac – 45ab – 15bc = 0
(15a)2 + (3b)2 + (5c)2 – (15a)(3b) – (3b)(5c) – (15a) (5c) = 0
1/2[(15a – 3b)2 + (3b – 5c)2 + (5c – 15a)2] = 0
15a = 3b , 3b = 5c , 5c = 15a
5a = b , 3b = 5c , c = 3a
a/1 = b/5 = c/3
a = λ, b = 5λ, c = 3λ
a, c, b are in AP
hyperbola passes through the point P(√2, √3) and has foci at (± 2, 0). Then the tangent to this hyperbola at P also passes through the point
C.
Equation of hyperbola is 
foci is (±2, 0) hence ae = 2, ⇒ a2e2 = 4
b2 = a2(e2 – 1)
∴ a2 + b2 = 4
Hyperbola passes through √2,√3
Sponsor Area
Mock Test Series
