Sponsor Area
Let A and B be two sets containing 2 elements and 4 elements respectively. The number of subsets of A × B having 3 or more elements is
256
220
219
211
C.
219
Given, n(A) =2, n(B) = B
The number of subsets of AXB having 3 or more elements,
=
Sponsor Area
The real number k for which the equation, 2x3 +3x +k = 0 has two distinct real roots in [0,1]
lies between 1 and 2
lies between 2 and 3
lies between -1 and 0
does not exist
D.
does not exist
Let f(x) = 2x3+3x+k
On differentiating w.r.t x, we get
f'(x) = 6x2 + 3> 0, ∀ x ε R
⇒ f(x) is strictly increasing function
⇒ f(x) = 0 has only one real root, so two roots are not possible.
The sum of first 20 terms of the sequence 0.7,0.77,0.777...... is
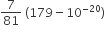
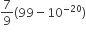
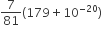
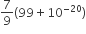
C.
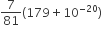
Let S = 0.7 + 0.77 +0.777 + .... upto 20 terms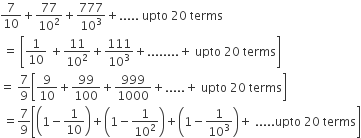
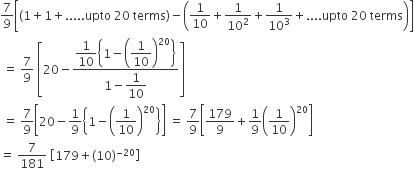
A ray of light along 
get reflected upon reaching X -axis, the equation of the reflected ray is
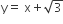
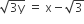
B.
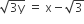
Given equation of line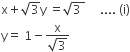
Slope of incident ray is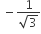 
So, slope of reflected ray must be 
and the point of incident 
So equation of reflected ray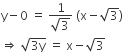
The number of values of k, for which the system of equations
(k+1) x + 8y = 4k
kx + (k+3)y = 3k -1
has no solution, is
infinite
1
2
3
B.
1
Condition for the system of equations has no solution,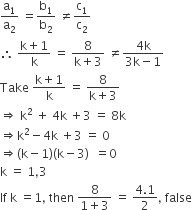
Therefore, k = 3
Hence, only one value of k exists.
Sponsor Area
Mock Test Series
