The equation esinx-e-sinx -4 = 0 has
-
infinite number of real roots
-
No real root
-
exactly one real root
-
exactly four real roots
B.
No real root
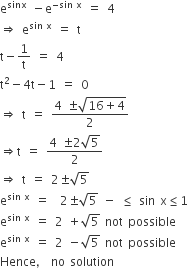
Sponsor Area
The equation esinx-e-sinx -4 = 0 has
infinite number of real roots
No real root
exactly one real root
exactly four real roots
B.
No real root
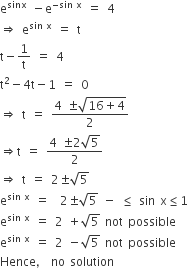
Sponsor Area
Statement 1: The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + ...... + (361 + 380 +400) is 8000.
Statement 2:  , for any natural number n.
, for any natural number n.
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is false
B.
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 has 20 terms whose sum is 8000 And statement 2 is true and supporting statement 1.
kth bracket is (k – 1)2 + k(k – 1) + k2 = 3k2 – 3k + 1.
The negation of the statement “If I become a teacher, then I will open a school” is
I will become a teacher and I will not open a school
Either I will not become a teacher or I will not open a school
Neither I will become a teacher nor I will open a school
I will not become a teacher or I will open a school
A.
I will become a teacher and I will not open a school
Let us assume that
p: I become a teacher' and
q: I will open a school
Then, we can easily as certain that
Negation of (p →q)
~(~p ∨ q) = p ∧ ~q
Which means that ' l' will become a teacher and I will not open a school.
Statement I An equation of a common tangent to the parabola  and the ellipse 2x2 +y2 =4 is
and the ellipse 2x2 +y2 =4 is  .
.
Statement II If the line  is a common tangent to the parabola
is a common tangent to the parabola  and the ellipse 2x2 +y2 =4, then m satisfies m4 +2m2 =24
and the ellipse 2x2 +y2 =4, then m satisfies m4 +2m2 =24
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is false
C.
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1

If n is a positive integer, then  is
is
an irrational number
an odd positive integer
an even positive integer
a rational number other than positive integers
A.
an irrational number


 appears in each of the terms.
appears in each of the terms.Sponsor Area
Mock Test Series