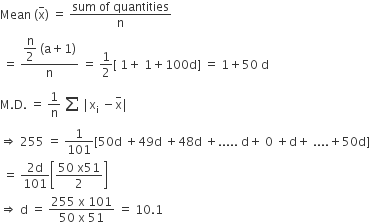
Sponsor Area
If the mean deviation of the numbers 1, 1 + d, 1+ 2d, ... , 1 + 100d from their mean is 255, then the d is equal to
10.0
20.0
10.1
20.2
C.
10.1
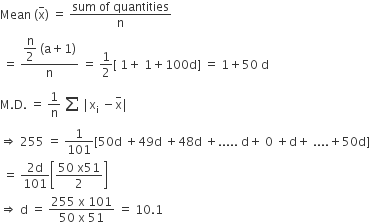
Sponsor Area
If the roots of the equation bx2+ cx + a = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is
greater than 4ab
less than 4ab
greater than -4ab
less than 4ab
C.
greater than -4ab
As, bx2 + cx + a = 0 has imaginary roots
So, c2< 4ab
Now, 3b2x2 + 6bcx + 2c2
= 3(bx + c)2– c2≥ – c2≥ – 4ab
Let A and B denote the statements
A: cos α + cosβ + cosγ = 0
B : sinα + sinβ + sinγ = 0
If cos(β – γ) + cos(γ – α) + cos(α – β) = – 3/2, then
A is true and B is false
A is false and B is true
both A and B are true
both A and B are false
C.
both A and B are true
cos(β–γ) + cos(γ – α) + cos(α – β) = –3/2
⇒ 2cos (β – γ) + 2cos(γ– α) + 2cos(α – β) = –3
⇒ Σ(cosβcosγ + 2Σsin α sinβ + 3 = 0
⇒ (cosα+cosβ + cosγ)2+ (sinα + sinβ +sinγ)2=0
⇒ cosα + cosβ + cosγ = 0
sinα + sinα + sinγ = 0
If A, B and C are three sets such that A ∩ B = A∩ C and A ∪ B = A ∪ C, then
A = B
A = C
B = C
A ∩ B = φ
C.
B = C
A ∪ B = A ∪ C
⇒ n (A ∪ B) = n(A ∪ C)
⇒ n(A) + n(B) – n(A ∩ B)
= n(A) + n(C) – n(A ∩C)
n(B) = n(C)
The projections of a vector on the three coordinate axis are 6, - 3, 2 respectively. The direction cosines of the vector are
6, –3, 2
6/5, -3/5, 2/5
6/7, -3/7, 2/7
-6/7, -3/7, 2/7
C.
6/7, -3/7, 2/7
Projection of a vector on coordinate axis are
x2-x1, y2-y1, z2-z1
x2-x1 = 6, y2-y1 = -3, z2-z1 = 2
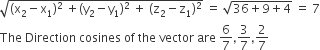
Sponsor Area
Mock Test Series
