Suppose a population A has 100 observations 101, 102, … , 200, and another population B has 100 observations 151, 152, … , 250. If VA and VB represent the variances of the two populations, respectively, then V_A/V_B is 

• 1

• 9/4

• 4/9

• 2/3

A.

1

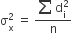(Here deviations are taken from the mean) Since A and B both have 100 consecutive integers, therefore both have same standard deviation and hence the variance. 

If the roots of the quadratic equation x² + px + q = 0 are tan30° and tan15°, respectively then the value of 2 + q − p is

• 2

• 3

• 0

• 1

Let W denote the words in the English dictionary. Define the relation R by :
R = {(x, y) ∈ W × W | the words x and y have at least one letter in common}. Then R is

• not reflexive, symmetric and transitive

• reflexive, symmetric and not transitive

• reflexive, symmetric and transitive

• reflexive, not symmetric and transitive

The value of 

• i

• 1

• -i

• -1

C.

-i

All the values of m for which both roots of the equations x² − 2mx + m² − 1 = 0 are greater than −2 but less than 4, lie in the interval

• −2 < m < 0

• m > 3

• −1 < m < 3 

• 1 < m < 4