+91-8076753736 [email protected]
logo
logo

JEE mathematics

Sponsor Area

Question
CBSEENMA11015622
Wired Faculty App

If the cube roots of unity are 1, ω, ω2 then the roots of the equation (x – 1)3 + 8 = 0, are

  • -1 , - 1 + 2ω, - 1 - 2ω2

  • -1 , -1, - 1

  • -1 , 1 - 2ω, 1 - 2ω2

  • -1 , 1 + 2ω, 1 + 2ω2

Solution

C.

-1 , 1 - 2ω, 1 - 2ω2

(x – 1)3 + 8 = 0
⇒ (x – 1) = (-2) (1)1/3
⇒ x – 1 = -2 or -2ω or -2ω2 or
n = -1 or 1 – 2ω or 1 – 2ω2 .

Sponsor Area

Question
CBSEENMA11015623
Wired Faculty App

Area of the greatest rectangle that can be inscribed in the ellipse straight x squared over straight a squared plus straight y squared over straight b squared space equals space 1

  • 2ab

  • ab

  • square root of ab

  • a/b

Solution

A.

2ab


Area of rectangle ABCD = (2acosθ)
(2bsinθ) = 2absin2θ
⇒ Area of greatest rectangle is equal to 2ab when sin2θ = 1.

Question
CBSEENMA11015624
Wired Faculty App

limit as straight n rightwards arrow infinity of space open square brackets 1 over straight n squared sec squared space 1 over straight n squared plus 2 over straight n squared space plus 2 over straight n squared sec squared 4 over straight n squared plus.....1 over straight n squared sec squared 1 close square brackets equal
  • 1 half sec space 1
  • 1 half cosec space 1

  • tan 1

  • 1 half tan space 1

Solution

D.

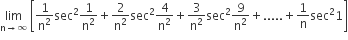1 half tan space 1 limit as straight n rightwards arrow infinity of space open square brackets 1 over straight n squared sec squared 1 over straight n squared plus 2 over straight n squared sec squared 4 over straight n squared plus 3 over straight n squared sec squared 9 over straight n squared plus..... plus 1 over straight n sec squared 1 close square brackets is equals
limit as straight n rightwards arrow infinity of space straight r over straight n squared space sec squared space straight r squared over straight n squared space equals space limit as straight n rightwards arrow infinity of 1 over straight n. straight r over straight n space sec squared straight r squared over straight n squared
rightwards double arrow space Given space limit space is space equal space to space value space of space integral space integral subscript 0 superscript 1 straight x space sec squared space straight x squared space dx or space 1 half integral subscript 0 superscript 1 space 2 straight x space sec space straight x squared space dx space equals space 1 half integral subscript 0 superscript 1 space sec squared space tdt space equals space 1 half left parenthesis tan space straight t right parenthesis subscript 0 superscript 1 space equals space 1 half space tan space 1

Question
CBSEENMA11015625
Wired Faculty App

If in a frequently distribution, the mean and median are 21 and 22 respectively, then its mode is approximately

  • 22.0

  • 20.5

  • 25.5

  • 24.0

Solution

D.

24.0

Mode + 2Mean = 3 Median
⇒ Mode = 3 × 22 – 2 × 21= 66 – 42= 24.

Question
CBSEENMA11015626
Wired Faculty App

Let P be the point (1, 0) and Q a point on the locus y2 = 8x. The locus of mid point of PQ is

  • y2 – 4x + 2 = 0

  • y2 + 4x + 2 = 0

  • x2 + 4y + 2 =

  • x2 – 4y + 2 = 0

Solution

A.

y2 – 4x + 2 = 0

P = (1, 0) Q = (h, k) such that
k2 = 8h
Let (α, β) be the midpoint of PQ
straight alpha space equals space fraction numerator straight h plus 1 over denominator 2 end fraction comma space straight beta space equals space fraction numerator straight k plus 0 over denominator 2 end fraction 2 straight alpha space minus 1 space equals straight h comma 2 straight beta space equals straight k left parenthesis 2 straight beta right parenthesis squared space equals space 8 space left parenthesis 2 straight alpha minus 1 right parenthesis rightwards double arrow straight beta squared space equals space 4 straight alpha space minus 2 rightwards double arrow space straight y squared minus 4 straight x space plus 2 space equals space 0

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation