+91-8076753736 [email protected]
logo
logo

JEE mathematics

Sponsor Area

Question
CBSEENMA11015657
Wired Faculty App

Let z, w be complex numbers such that z iw + = 0 and arg zw = π. Then arg z equals

  • π/4

  • 5π/4

  • 3π/4

  • π/2

Solution

C.

3π/4

Since z + iw = 0 ⇒ z = −iw
⇒ z = iw
⇒ w = -iz
Also arg(zw) = π
⇒ arg (-iz2) = π
⇒ arg (-i) + 2 arg(z) = π
negative straight pi over 2 space plus space 2 arg space left parenthesis straight z right parenthesis space equals space straight pi space space left parenthesis because space arg space left parenthesis negative straight i right parenthesis space equals space minus straight pi divided by 2 right parenthesis 2 space arg space left parenthesis straight z right parenthesis space equals space fraction numerator 3 straight pi over denominator 2 end fraction arg space left parenthesis straight z right parenthesis space equals space fraction numerator 3 straight pi over denominator 4 end fraction

Sponsor Area

Question
CBSEENMA11015658
Wired Faculty App

If z = x – i y and z1/3 = p+ iq , then 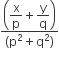fraction numerator begin display style open parentheses straight x over straight p plus straight y over straight q close parentheses end style over denominator left parenthesis straight p squared plus straight q squared right parenthesis end fraction is equal to 

  • 1

  • -2

  • 2

  • -1

Solution

B.

-2

D.

-1

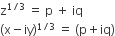straight z to the power of 1 divided by 3 end exponent space equals space straight p space plus space iq left parenthesis straight x minus iy right parenthesis to the power of 1 divided by 3 end exponent space equals space left parenthesis straight p plus iq right parenthesis      therefore,(Qz = x − iy)
(x - iy) = (p + iq)3
⇒ (x - iy) = p3 +(iq)3 + 3p2qi + 3pq2i2
⇒ (x - iy) = p3 - iq3 + 3p2qi - 3pq2
⇒ (x - iy) = (p3 - 3pq2 ) + i (3p2 q - q3 ) On comparing both sides, we get
⇒ x = (p3 - 3pq2) and - y = 3p2 q - q3
⇒ x = p(p2 - 3q2 ) and y = q(q2 - 3p2 )

Question
CBSEENMA11015659
Wired Faculty App

If |z2-1|=|z|2+1, then z lies on

  • the real axis

  • an ellipse

  • a circle

  • the imaginary axis

Solution

B.

an ellipse

Given that
|z2- 1| = |z|2+ 2
|z2 + (-1)| = |z2| + |-1|
It shows that the origin, -1 and z2 lies on a line and z2 and -1 lies on one side of the origin, therefore
z2 is a negative number. Hence z will be purely imaginary. So we can say that z lies on y-axis.

Question
CBSEENMA11015660
Wired Faculty App

If a1, a2, a3 , ....,an , .... are in G.P., then the value of the determinant open square brackets table row cell log space straight a subscript straight n end cell cell log subscript straight n plus 1 end subscript end cell cell log subscript straight n plus 2 end subscript end cell row cell log space straight a subscript straight n plus 3 end subscript end cell cell log space straight a subscript straight n plus 4 end subscript end cell cell log space straight a subscript straight n plus 5 end subscript end cell row cell log space straight a subscript straight n plus 6 end subscript end cell cell log space straight a subscript straight n plus 7 end subscript end cell cell log space straight a subscript straight n plus 8 end subscript end cell end table close square brackets is

  • 0

  • -2

  • 1

  • 2

Solution

A.

0

Question
CBSEENMA11015661
Wired Faculty App

Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation

  • x2 + 18x +16 = 0

  • x2-18x-16 = 0

  • x2+18x-16 =0

  • x2-18x +16 =0

Solution

D.

x2-18x +16 =0

Let α and β be two numbers whose arithmetic mean is 9 and geometric mean is 4.
∴ α + β = 18 ........... (i)
and αβ =16 ........... (ii)
∴ Required equation is x2 - (α + β)x + (αβ) = 0 ⇒ x2 - 18x + 16 = 0 [using equation (i) and equation (ii)]

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation