ICSE physics
Sponsor Area
Mention any two difference between the mass and weight of a body.
Difference between mass and weight of the body:
|
Mass |
Weight |
|
1. It is a scalar quantity. 2. It is the quantity of matter contained in a body.
|
1. It is a vector quantity. 2. It is the force with which the earth attracts a body. |
Sponsor Area
Define Newton, the S.I. unit of force. State its relationship with the C.G.S. unit of force.
One Newton is the amount of force required to produce an acceleration of 1 m/s2 in a body of mass 1 kg.
1 Newton = 1 kg x 1 m/s2
= 1000 g x 100 cm/s2
= 105 g cm/s2
= 10 5 dyne
That is, 1 N = 105 dyne
State the amount of work done by an object when it moves in a circular path for one complete rotation. Give a reason to justify your answer.
The amount of work done will be equal to zero. This is because, work is said to be done only when there is a displacement produced. In case of a body moving in a circular path, the body comes to its original place, therefore, there is no displacement and hence work is zero.
Calculate the height through which a body of mass 0.5 kg should be lifted if the energy spent for doing so is 1.0 Joule.
Given,
Mass, m = 0.5 kg
P.E = 1.0 g
Acceleration due to gravity, g = 10 m/s2
P.E = mgh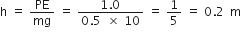
Show that for the free fall of a body, the sum of the mechanical energy at any point in its path is constant.
Let a body of mass m fall freely under gravity from height h above ground.
Let, A B and C be the positions of body.
Let x be the distance fallen from A to B.
At position A:
K.E= 0 (body is at rest)
P.E = mgh
Therefore,
Total energy = 0 + mgh = mgh … (i)
At position B:
Let v1 be velocity of body, then u = 0
S= x
Using equation of motion, we have
V2 = u2 + 2as
V12 = 0 + 2 gx
V12 = 2 gx 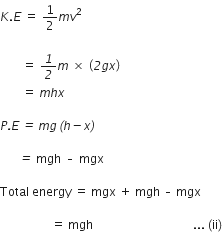
At position C:
Let velocity of body be v.
Then, u = 0 and S = h
From equation,
V2 = u2 + 2gs
V2 = 0 + 2gh
V2 = 2gh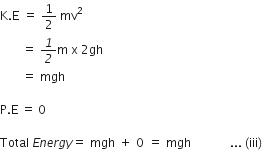
Therefore, from equations (i), (ii) and (iii), it is clear that the sum of mechanical energy remains same at any point in the path of free fall of a body.
Sponsor Area
Mock Test Series
Mock Test Series





