Question

Two electric bulbs P and Q have their resistances in the ratio of 1: 2. They are connected in series across a battery.Find the ratio of the power dissipation in these bulbs.

Solution

Let ratio be x

R_p = x (Resistance of bulb P)

R_q = 2x (Resistance of bulb Q)

We know, P = VI = V.V/R

$\frac{P_{p}}{P_{q}} = \frac{V_{2}}{R_{p}} x \frac{R_{q}}{V_{2}} (In series Potential will be same) \frac{P_{p}}{P_{q}} = \frac{2 x}{x} 2 : 1$

Question

Wired Faculty App

A 10 V cell of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38 Ω as shown in the figure. Find the value of current in the circuit.

Solution

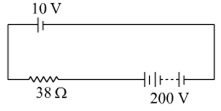
WiredFaculty

The positive terminals are connected to the offsite ends of the resistor, they send the current in opposite directions.

Hence, the net emf = 200-10 = 190 V

∴ current in the circuit I = E/R

= 190V / 38 Ω

= 5 A

Question

Wired Faculty App

In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9 ohm is used in the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell.

Solution

Potentiometer at open circuit ℓ₁ = 350

R = 9

ℓ₂ = 300

$r = R (\frac{I_{1}}{l_{2}} - 1) r = 9 (\frac{350}{300} - 1) = 1.5 Ω$

Question

Wired Faculty App

Four point charges Q, q, Q and q are placed at the corners of a square of side ‘a’ as shown in the figure
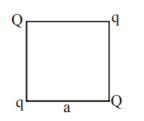
Find the
(a) resultant electric force on a charge Q,
(b) the potential energy of this system.

Solution

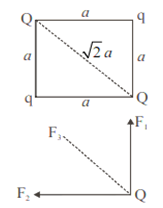
WiredFaculty

$F_{1} = \frac{1}{4 {πε}_{0}} = \frac{qQ}{a^{2}} F_{2} = \frac{1}{4 {πε}_{0}} \frac{qQ}{a^{2}} F_{3} = \frac{1}{4 {πε}_{0}} \frac{QQ}{(\sqrt{2 a)^{2}}} = \frac{1}{4 {πε}_{0}} \frac{Q^{2}}{2 a^{2}}$

F₁ and F₂ are perpendicular to each other so their resultant will be

$F' = \sqrt{F_{1}^{2} + F_{2}^{2} + 2 F_{1} F_{2} \cos 90^{o}} F_{1} = F_{2} F' = \sqrt{2} \frac{1}{4 {πε}_{0}} \frac{qQ}{a^{2}}$

F₃ and resultant of F₁ and F₂ will be in the same direction

Net force

F = F' + F₃

$F = \frac{Q}{4 {πε}_{0}} [\frac{\sqrt{2 q}}{a^{2}} + \frac{Q}{2 a^{2}}] = \frac{Q}{4 {πε}_{0}} [\frac{2 \sqrt{2 q} + Q}{2 a^{2}}] F = \frac{Q}{4 {πε}_{0}} [\frac{2 \sqrt{2 q} + Q}{2 a^{2}}]$

(b) The potential energy of the given system,

$W = \frac{4 KQq}{a} + \frac{{Kq}^{2}}{\sqrt{2} a} + \frac{{KQ}^{2}}{\sqrt{2} a} K = \frac{1}{4 {πε}_{0}}$

Question

Wired Faculty App

Three point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side ‘l’ as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
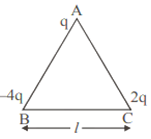
(b) Find out the amount of the work done to separate the charges at infinite distance.

Solution

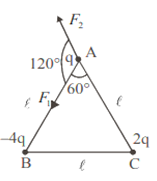
WiredFaculty

$| {\vec{F}}_{1} | = \frac{1}{4 {πε}_{0}} \frac{(4 q) (q)}{l^{2}} F_{1} = \frac{1}{4 {πε}_{0}} \frac{(4 q^{2})}{l^{2}} F_{1} = \frac{1}{{πε}_{0}} \frac{q^{2}}{l^{2}} {\vec{F}}_{2} | = \frac{1}{4 {πε}_{0}} \frac{(2 q) (q)}{l^{2}} F_{2} = \frac{1}{2 {πε}_{0}} \frac{q^{2}}{l^{2}} angle between \vec{F_{1}} and \vec{F_{2}} is 120^{o} \vec{F} = \sqrt{F_{1}^{1} + F_{2}^{2} + 2 F_{1} F_{2} \cos 120^{o}} F_{1} = 2 F_{2} F = \sqrt{(2 F_{2})^{2} + F_{2}^{2} + 4 F_{2}^{2} \cos 120^{0}} F = \sqrt{4 F_{2}^{2} + F_{2}^{2} - 2 F_{2}^{2}} F = \sqrt{3 F_{2}^{2}} F = \sqrt{3 F_{2}^{2}} F = \sqrt{3} \frac{1}{2 {πε}_{0}} \frac{q^{2}}{l^{2}}$

(b) The amount of work done to separate the charges at infinity will be equal to potential energy.

$U = \frac{1}{4 {πε}_{0} l} [q x (- 4 q) + (q x 2 q) + (- 4 q x 2 q) U = \frac{1}{4 {πε}_{0} l} [- 4 q^{2} + 2 q^{2} - 8 q^{2}] U = \frac{1}{4 {πε}_{0} l} [- 10 q^{2}] U = - \frac{1}{4 {πε}_{0} l} [10 q^{2} unit$

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

CBSE physics

Two electric bulbs P and Q have their resistances in the ratio of 1: 2. They are connected in series across a battery.Find the ratio of the power dissipation in these bulbs.

A 10 V cell of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38 Ω as shown in the figure. Find the value of current in the circuit.

In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9 ohm is used in the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell.

Four point charges Q, q, Q and q are placed at the corners of a square of side ‘a’ as shown in the figure
Find the
(a) resultant electric force on a charge Q,
(b) the potential energy of this system.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

CBSE physics

Two electric bulbs P and Q have their resistances in the ratio of 1: 2. They are connected in series across a battery.Find the ratio of the power dissipation in these bulbs.

A 10 V cell of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38 Ω as shown in the figure. Find the value of current in the circuit.

In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9 ohm is used in the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell.

Four point charges Q, q, Q and q are placed at the corners of a square of side ‘a’ as shown in the figureFind the(a) resultant electric force on a charge Q,(b) the potential energy of this system.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Four point charges Q, q, Q and q are placed at the corners of a square of side ‘a’ as shown in the figure
Find the
(a) resultant electric force on a charge Q,
(b) the potential energy of this system.