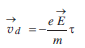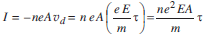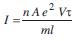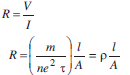Deduce the expression for the electrostatic energy stored in a capacitor of capacitance ‘C’ and having charge ‘Q’.
How will the (i) energy stored and (ii) the electric field inside the capacitor be affected when it is completely filled with a dielectric material of dielectric constant ‘K’?
When a capacitor is charged by a battery, work is done by the charging battery at the expense of its chemical energy. This work is stored in the capacitor in the form of electrostatic potential energy.
Consider a capacitor of capacitance C. Initial charge on capacitor is zero. Initial potential difference between capacitor plates =0. Let a charge Q be given to it in small steps. When charge is given to capacitor, the potential difference between its plates increases.
Potential difference between its plates, V= q/C
Work done to give an infinitesimal charge dq to the capacitor is given by,

If V is the final potential difference between capacitor plates, then Q = CV

Work is stored in the form of electrostatic potential energy.
Electrostatic potential energy, U = 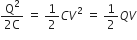
When battery is disconnected,
i) Energy stored will decrease.
Energy becomes, U = 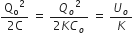
So, energy is reduced to 1/K times its initial energy.
i) In the presence of dielectric, electric field becomes, E = 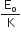

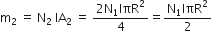
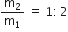








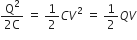
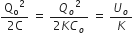
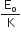
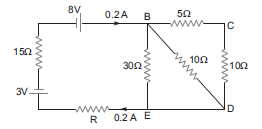

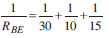
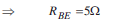
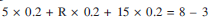
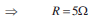
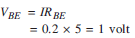
 t is applied across it. Since all the components are connected in series, the current flowing through all is same.
t is applied across it. Since all the components are connected in series, the current flowing through all is same.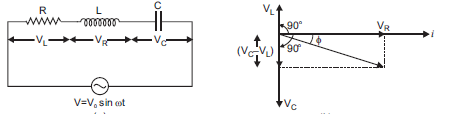
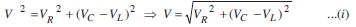
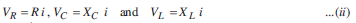

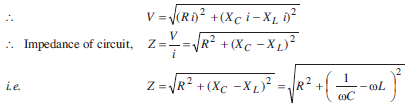
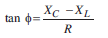
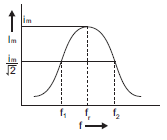
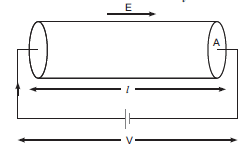
 and vd is given by,
and vd is given by,