Let the total number of rotten apples in a heap = n

Total number of apples in a heap = 900

probability of selecting a rotten apple from a heap = 0.18

Now.

$$\begin{gathered} \mathrm{P}(\mathrm{selecting} \mathrm{a} \mathrm{rotten} \mathrm{apple}) = \frac{\mathrm{Number} \mathrm{of} \mathrm{rotten} \mathrm{apples}}{\mathrm{Total} \mathrm{number} \mathrm{of} \mathrm{apples}} \\ \Rightarrow 0.18 = \frac{\mathrm{n}}{900} \\ \Rightarrow \mathrm{n} = 0.18 \mathrm{x} 900 \\ \Rightarrow \mathrm{n} = 162 \\ \mathrm{Hence}, \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{rotten} \mathrm{apples} \mathrm{is} 162. \end{gathered}$$

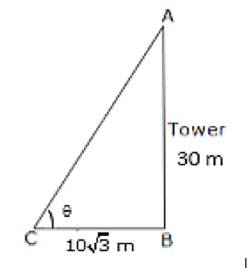
Let AB be the tower and BC  be its shadow.

$$\begin{gathered} \mathrm{AB} = 30 \mathrm{m}, \mathrm{BC} = 10\sqrt{3} \mathrm{m} \\ \mathrm{In} ∆\mathrm{ABC}, \\ \mathrm{tan\theta } = \frac{\mathrm{AB}}{\mathrm{BC}} \\ \Rightarrow \mathrm{tan\theta } = \frac{30}{10\sqrt{3}} \\ \Rightarrow \mathrm{tan\theta } =\frac{3}{\sqrt{3}} \\ \tan \mathrm{\theta } = \sqrt{3} \\ \mathrm{But}, \tan 60° =\sqrt{3} \\ \therefore \mathrm{\theta } = 60° \\ \mathrm{Thus}, \mathrm{the} \mathrm{angle} \mathrm{of} \mathrm{elevation} \mathrm{of} \mathrm{sun} \mathrm{is} 60°. \end{gathered}$$

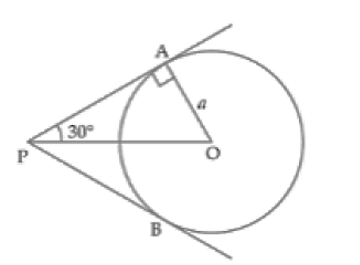
In the figure, PA and PB are two tangents from an external point P to a circle with centre O and radius = a

$$\begin{gathered} \angle \mathrm{APB} = 60° ( \mathrm{given} ) \\ \Rightarrow \angle \mathrm{APQ} = 30° ( \mathrm{tangents} \mathrm{are} \mathrm{equally} \mathrm{inclined} \mathrm{to} \mathrm{the} \mathrm{line} \\ \mathrm{joining} \mathrm{the} \mathrm{point} \mathrm{and} \mathrm{the} \mathrm{centre}. ) \\ \mathrm{Now}, \mathrm{OA} \perp \mathrm{AP} \\ \mathrm{In} \mathrm{right} \mathrm{angled} \mathrm{triangle} \mathrm{OAP}, \\ \sin 30° = \frac{\mathrm{OA}}{\mathrm{OP}} \\ \Rightarrow \frac{1}{2} = \frac{\mathrm{a}}{\mathrm{OP}} \\ \Rightarrow \mathrm{OP} = 2\mathrm{a} \end{gathered}$$

Let a be the first term and d be the common difference of the given A.P.

$$\begin{gathered} \therefore {\mathrm{a}}_{21 }- {\mathrm{a}}_7 = 84 \\ \Rightarrow \left(\mathrm{a} + 20\mathrm{d}\right) - \left(\mathrm{a} + 6\mathrm{d}\right) = 84 \\ \Rightarrow \mathrm{a} + 20\mathrm{d} -\mathrm{a} - 6\mathrm{d} = 84 \\ \Rightarrow 14\mathrm{d} = 84 \\ \Rightarrow \mathrm{d} = 6 \\ \mathrm{Hence}, \mathrm{the} \mathrm{common} \mathrm{difference} \mathrm{is} 6. \end{gathered}$$

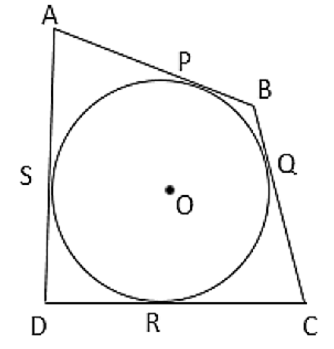
Since tangents drawn from an external point to a circle are equal in length, we have

AP = AS    ........(i)

BP = BQ   ........(ii)

CR = CQ   ........(iii)

DR = DS   ........(iv)

Adding (i), (ii), (iii), (iv), we get 

    AP + BP + CR + DR = AS + BQ + CQ + DS

$\Rightarrow$  ( AP + BP ) + ( CR + DR ) = ( AS + DS ) + ( BQ + CQ )

$\Rightarrow \; AB\; +\; CD\; =\; AD\; +\; BC$

$\Rightarrow \; AB\; +\; CD\; =\; BC\; +\; DA$