CBSE mathematics
Sponsor Area
In Fig. , PQ is tangent at point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.
In the given figure,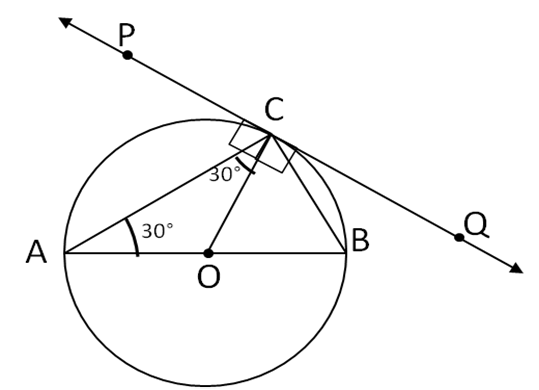
In Δ ACO,
OA=OC (Radii of the same circle)
Therefore,
ΔACO is an isosceles triangle.
∠CAB = 30° (Given)
∠CAO = ∠ACO = 30° (angles opposite to equal sides of an isosceles triangle are equal)
∠PCO = 90° …(radius is drawn at the point of
contact is perpendicular to the tangent)
Now ∠PCA = ∠PCO – ∠CAO
Therefore,
∠PCA = 90° – 30° = 60°
Sponsor Area
For what value of k will k+9, 2k-1 and 2k+7 are the consecutive terms of an A.P?
If k+9, 2k-1 and 2k+7 are the consecutive terms of A.P, then the common difference will be the same.
∴ (2k – 1) – (k + 9) = (2k + 7) – (2k – 1)
∴ k – 10 = 8
∴ k = 18
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
Let AB be the ladder and CA be the wall.
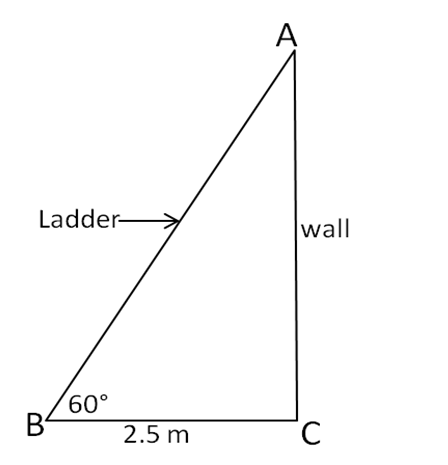The ladder makes an angle of 60o with the horizontal.∴ ΔABC is a 30o-60o-90o, right triangle.
Given: BC = 2.5 m, ∠ABC = 60°
AB = 5 cm and ∠BAC = 30°
From Pythagoras Theorem, we have
AB2 = BC2 + CA2
52 = (2.5)2 + (CA)2
(CA)2 = 25 – 6.25 = 18.75 m
Hence, length of the ladder is 
A card is drawn at random from a well -shuffled fled pack of 52 playing cards. Find the probability of getting neither a red card nor a queen.
1.
If -5 is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p(x2 + x)k = 0 has equal roots, find the value of k.
We Given -5 is a root of the quadratic equation 2x2+px-15 =0
, -5 satisfies the given equation.
∴ 2 (-5)2 +p(-5)-15=0
50-5p-15 =0
35-5p=0
5p=35 ⇒ p=7
Substituting p=7 in (x2+x)+k =0, we get
7(x2+x)+k =0
7x2+7x+k=0
The roots of the equation are equal
∴ Discriminant =b2-4ac =0
Here, a= 7, b=7,c=k
b2-4ac=0
∴(7)2-4(7)(k) =0
49-28k =0
28k=49
k= 49/28
=7/4
Sponsor Area
Mock Test Series
Mock Test Series