CBSE mathematics
Sponsor Area
If the quadratic equation has ![]() two roots, then find the value of p.
two roots, then find the value of p.
The given quadratic equation has ![]() two equal roots.
two equal roots.
therefore,
by using the discriminant method

⇒ 20p2 - 60p = 0
⇒ 20p (p - 3) = 0
⇒ p = 0 or p - 3 = 0
⇒ p = 0 or p = 3
p cannot be zero.
Hence, the value of p is 3.
Sponsor Area
In Given figure, a tower AB is 20 m high and BC, its shadow on the ground, is m ![]() long. Find the sun's altitude.
long. Find the sun's altitude.
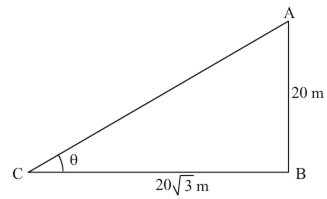
Let the sun's altitude be θ.
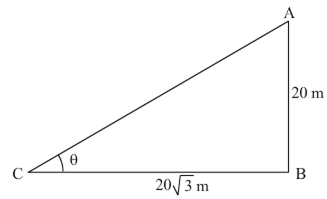 In ΔABC,
In ΔABC,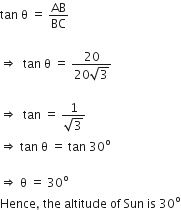
The different dice are tossed together. Find the probability that the product of the two number on the top of the dice is 6.
When two dice are thrown simultaneously, the possible outcomes can be listed as:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
( 1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
∴ Total number of possible outcomes = 36
The outcomes favourable to the event the product of the two number of the top of the dice is 6 denoted by E are (1, 6), (2, 3), (3, 2) and (6, 1)
∴ Number of favourable outcomes = 4
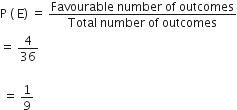
In the given figure, PQ is a chord of a circle with centre O and PT is tangent. If ∠QPT = 60o, find ∠ PRQ.
PQ is the chord of the circle and PT is tangent.
We know that the tangent to a circle is perpendicular to the radius through the point of contact.
∴ ∠ OPT = 90o
Now, Given
∠ QPT = 60o
∴ ∠ OPQ = ∠OPT - ∠QPT
⇒ ∠ OPQ = 90o - 60o = 30o
In Δ OPQ,
OP= OR (Radii of the same circle)
∠ OQP = ∠ OPQ = 30o (in a triangle, equal sides have equal angles opposite to them.)
Now,
∠ OQP + ∠OPQ + ∠POQ = 180o [Angle sum property]
⇒ 30o + 30o + ∠POQ = 180o
⇒ ∠POQ = 180o - 60o = 120o
⇒ Reflex ∠POQ = 360o -120o = 240o
We know that the angle subtended by an arc of a circle at the centre is twice the angle subtended by it any point on the remaining part of the circle.
Therefore,
Reflex ∠POQ = 2 ∠PRQ
⇒ 240o = 2 ∠PRQ
⇒ ∠PRQ = 240 / 2 = 120o
Hence, the measure of angle PRQ is 120o.
In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120o, then prove that OR = PR + RQ.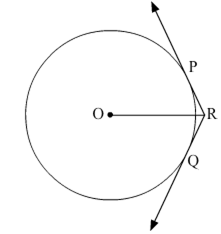
Given: RQ and RP are tangents drawn from an external point R to the circle with centre O such that ∠PRQ = 120o
To prove, PR + PQ = OR
Construction, Join OP and OQ.

Proof:
∠OPR = ∠OQR = 90o
(Radius of the circle is perpendicular to the tangent to the circle through the point contact)
We Know that the centre lies on the bisector of the angle between the two tangents.
So, ∠PRO = ∠QRO = 1/2 ∠PRQ = 60o
Now, In ΔPRO,

Sponsor Area
Mock Test Series
Mock Test Series





