CBSE mathematics
Sponsor Area
The probability that a number selected at random from the numbers 1, 2, 3, ..., 15 isa multiple of 4, is
C.
Sponsor Area
Two circles touch each other externally at P. AB is a common tangent to the circlestouching them at A and B. The value of APB is
D.

If k, 2k- 1 and 2k + 1 are three consecutive terms of an A.P., the value of k is
2
3
-3
5
B.
3
In a family of 3 children, the probability of having at least one boy is
A.
There are in all 23 = 8 combinations or outcomes for the gender of the 3 children
The 8 combinations are as follows
BBB, BBG, BGB, BGG, GBB, GBG, GGB, GGG
Thus the probability of having at least one boy in a family is
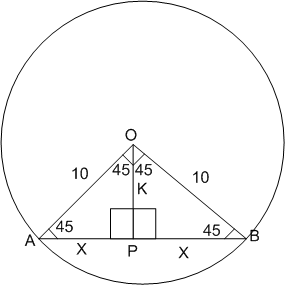
A chord of a circle of radius 10 cm subtends a right angleat its centre. The length of the chord (in cm) is
5
10
10
B.
10
Sponsor Area
Mock Test Series
Mock Test Series





