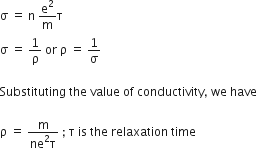Two long, straight, parallel conductors carry steady currents, I1 and I2 , separated by a distance . If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
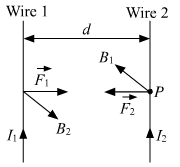

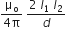
According to Fleming's left-hand rule, the force on wire 2 acts in the plane of paper perpendicular to wire 2, directed towards wire 1. Similarly, wire 1 also experiences the same force towards wire 2. Thus, both the conducting wires attract each other with the same force F.
One ampere can be defined as the amount of current flowing through two parallel conductors, which are in the same direction or opposite directions, placed at a distance of one metre in free space, and both the wires attract or repel each other with a force of 2 x 10-7 per metre of their lengths.






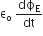 , where
, where  is the electric flux produced during charging of the capacitor plates.
is the electric flux produced during charging of the capacitor plates. 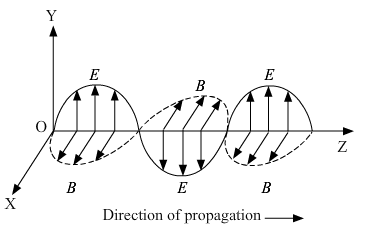
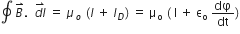
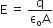 , is perpendicular to the surface of the plate.
, is perpendicular to the surface of the plate. 
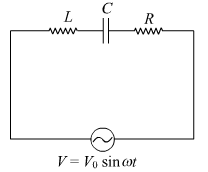
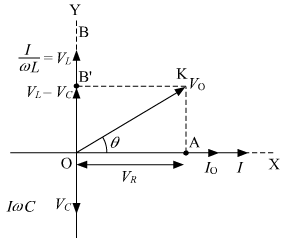
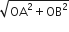
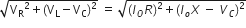
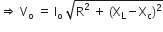
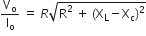
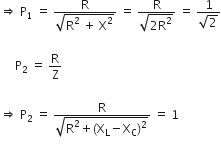
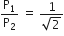
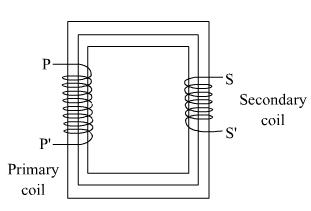
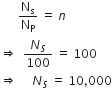
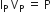
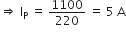
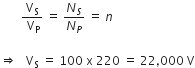
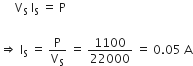
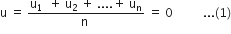
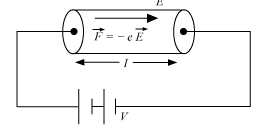
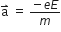 ... (2)
... (2) 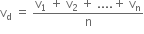
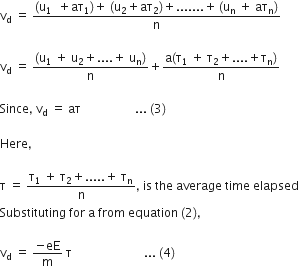

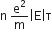

 is the conductivity of the material through whic the current is flowing,
is the conductivity of the material through whic the current is flowing,