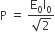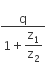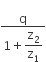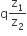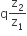TextBook Solutions for Mizoram Board Class 12 Physics Physics Part I Chapter 7 Alternating Current

The teachers of Geeta’s school took the students on a study trip to a power generating station, located nearly 200 km away from the city. The teacher explained that electrical energy is transmitted over such a long distance to their city, in the form of alternating current (ac) raised to a high voltage. At the receiving end in the city, the voltage is reduced to operate the devices. As a result, the power loss is reduced. Geeta listened to the teacher and asked questions about how the ac is converted to a higher or lower voltage.

1. Name the device used to change the alternating voltage to a higher or lower value. State one cause for
   power dissipation in this device.
2. Explain with an example, how power loss is reduced if the energy is transmitted over long distances as an alternating current rather than a direct current.
3. Write two values each shown by the teachers and Geeta.

A device X is connected across an ac source of voltage V=V₀sin ωt. The current through X is given as $\mathrm{I} - {\mathrm{I}}_0\sin \left(\mathrm{\omega t} + \frac{\mathrm{\pi }}{2}\right)$

1. Identify the device X and write the expression for its reactance.
2. Draw graphs showing a variation of voltage and current with time over one cycle ac, for X.
3. How does the reactance of the device X vary with the frequency of the ac? Show this variation graphically.
4. Draw the phasor diagram for the device X.

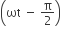In an a.c. circuit the voltage applied is E = E₀ sinπt. The resulting current in the circuit is I = I₀ sin .The power consumption in the circuit is given by

• 

• P = zero

• 
• 

A current I flows along the length of an infinitely long, straight, thin walled pipe. Then 

• the magnetic field is zero only on the axis of the pipe

• the magnetic field is different at different points inside the pipe

• the magnetic field at any point inside the pipe is zero

• the magnetic field at all points inside the pipe is the same, but not zero

In a series resonant LCR circuit, the voltage across R is 100 volts and R = 1 kΩ with C = 2µF. The resonant frequency ω is 200 rad/s. At resonance the voltage across L is

• 4 × 10−3 V

• 2.5 × 10⁻² V

• 40 V

• 250 V

Two voltameters one of copper and another of silver, are joined in parallel. When a total charge q flows through the voltameters, equal amount of metals are deposited. If the electrochemical equivalents of copper and silver are z₁ and z₂ respectively the charge which flows through the silver voltameter is

A circuit has a resistance of 12 Ω and an impedance of 15 Ω. The power factor of the circuit will be

• 0.8

• 0.4

• 1.25

• 0.125

The phase difference between the alternating current and emf is π/2. Which of the following cannot be the constituent of the circuit?

• C alone

• R.L

• L.C

• L alone

Alternating current can not be measured by D.C. ammeter because

• A.C. cannot pass through D.C.

• A.C. changes direction

• average value of current for complete cycle is zero

• D.C. ammeter will get damaged.

In an LCR series a.c. circuit, the voltage across each of the components, L, C and R is 50 V. The voltage across the LC combination will be

• 50 V

• 50√2 V

• 100 V

• 0 V(zero)