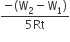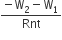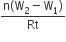Physics Part I Chapter 6 Electromagnetic Induction

Principle − AC generator based on the phenomenon of electromagnetic induction.

Construction:

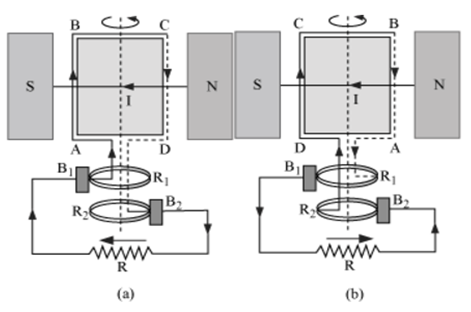
Main parts of an ac generator:

1. Armature − Rectangular coil ABCD

2. Filed Magnets − Two pole pieces of a strong electromagnet

3. Slip Rings − The ends of coil ABCD are connected to two hollow metallic rings R₁ and R₂.

4. Brushes − B₁ and B₂ are two flexible metal plates or carbon rods. They are fixed and are kept in tight contact with R₁ and R₂ respectively.

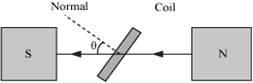
Theory and Working − As the armature coil is rotated in the magnetic field, angle θ between the field and normal to the coil changes continuously. Therefore, magnetic flux linked with the coil changes. An emf is induced in the coil. According to Fleming’s right-hand rule, current induced in AB is from A to B and it is from C to D in CD. In the external circuit, current flows from B₂ to B₁.

To calculate the magnitude of emf induced:

Suppose

A → Area of each turn of the coil

N → Number of turns in the coil

$\overrightarrow{\mathrm{B}}$→ Strength of magnetic field

θ → Angle which normal to the coil makes with at any instant t

∴ Magnetic flux linked with the coil in this position:

$\mathrm{\Phi } = \mathrm{N} (\overrightarrow{\mathrm{B}}.\overrightarrow{\mathrm{A}})$= NBA cosθ= NBA cosωt …(i)

Where, ‘ω’ is angular velocity of the coil

As the coil rotates, angle θchanges. Therefore, magnetic flux Φ linked with the coil changes and hence, an emf is induced in the coil. At this instant t, if e is the emf induced in the coil, then

$$\begin{gathered} \mathrm{e} = - \frac{\mathrm{d\theta }}{\mathrm{dt}} =-\frac{\mathrm{d}}{\mathrm{dt}} (\mathrm{NAB} \cos \mathrm{\omega t}) \\ = -\mathrm{NAB}\frac{\mathrm{d}}{\mathrm{dt}}(\cos \mathrm{\omega t}) \\ =-\mathrm{NAB} (-\sin \mathrm{\omega t}) \mathrm{\omega } \end{gathered}$$

e = B_v.V.l

=$$\begin{gathered} 5 x {10}^{-4} \sin 30 x 900 x \frac{5}{18} x 20 \\ = 1.25 V \end{gathered}$$

D.

12^e–5t V

B.

C.

-10 V

C.

5 × 10⁻⁵

B.

0.1 s

C.

1µF

B.

B.

depends on the intensity of the radiation

The emf induced between ends of conductor

C.

13.89

Energy stored in the inductor, 
U = 25 x 10^-3 J

Current, I = 60 mA
Energy stored in inductor $$\begin{gathered} U = \frac{1}{2}L{I}^2 \\ 25 x {10}^{-3} = \frac{1}{2} x L x (60 x {10}^{-3}{)}^2 \\ L = \frac{25 x 2 x {10}^6 x {10}^{-3}}{3600} = 13.89 H \end{gathered}$$

A.

$1:\sqrt{2}$

Suppose magnetic field is produced due to each coil is B.The coils are kept perpendicular hence, the angle between these is 90⁰.

Therefore the resultant magnetic field is given by :   $$\begin{gathered} \frac{\mathrm{B}}{\sqrt{2\mathrm{B}}}=1:\sqrt{2} \\ \mathrm{Hence} \mathrm{the} \mathrm{ratio} \mathrm{of} \mathrm{magnetic} \mathrm{field} \mathrm{is} \mathrm{due} \mathrm{to} \mathrm{one} \mathrm{coil} \mathrm{and} \mathrm{the} \mathrm{resultant} \mathrm{magnetic} \mathrm{field} \mathrm{is} \mathrm{given} \mathrm{by} \\ =\sqrt{{\mathrm{B}}^2 + {\mathrm{B}}^2 + 2\mathrm{B}.\mathrm{B} \cos {90}^0 } \\ =\sqrt{2{\mathrm{B}}^2+2{\mathrm{B}}^2\times 0} \\ =\sqrt{2{\mathrm{B}}^2} = \mathrm{B}\sqrt{2} \end{gathered}$$

B.

120 V

The magnetic flux linked with the primary coil is given by

$\mathrm{\varphi } = {\mathrm{\varphi }}_{\mathrm{o}} + 4\mathrm{t}$

So voltage across primary

$$\begin{gathered} {\mathrm{V}}_{\mathrm{P}} =\frac{\mathrm{d\varphi }}{\mathrm{dt}} \\ = \frac{\mathrm{d} }{\mathrm{dt}}\left({\mathrm{\varphi }}_{\mathrm{o}} + 4 \mathrm{t}\right) \\ {\mathrm{V}}_{\mathrm{P}} = 4 \mathrm{volt} ( \mathrm{as} {\mathrm{\varphi }}_{\mathrm{o}} = \mathrm{constant} ) \end{gathered}$$

Also we have

N_P = 50 and N_S = 1500

From relation

$$\begin{gathered} \frac{{\mathrm{V}}_{\mathrm{S}}}{{\mathrm{V}}_{\mathrm{P}}} = \frac{{\mathrm{N}}_{\mathrm{S}}}{{\mathrm{N}}_{\mathrm{P}}} \\ \Rightarrow {\mathrm{V}}_{\mathrm{S}} = {\mathrm{V}}_{\mathrm{P}} \frac{{\mathrm{N}}_{\mathrm{S}}}{{\mathrm{N}}_{\mathrm{P}}} \\ \Rightarrow {\mathrm{V}}_{\mathrm{S}} = 4 \left(\frac{1500}{50}\right) \\ \Rightarrow {\mathrm{V}}_{\mathrm{S}} = 120 \mathrm{V} \end{gathered}$$

C.

90%

The efficiency of the transformer 

$= \frac{\mathrm{Energy} \mathrm{obtained} \mathrm{from} \mathrm{the} \mathrm{secoindary} \mathrm{coil}}{\mathrm{Energy} \mathrm{given} \mathrm{to} \mathrm{the} \mathrm{primary} \mathrm{coil}}$

$$\begin{gathered} \mathrm{\eta } = \frac{\mathrm{Output} \mathrm{power}}{\mathrm{Input} \mathrm{power}} \\ \Rightarrow \mathrm{\eta } = \frac{{\mathrm{V}}_{\mathrm{s}} {\mathrm{I}}_{\mathrm{s}}}{{\mathrm{V}}_{\mathrm{p}} {\mathrm{I}}_{\mathrm{p}}} \end{gathered}$$

Given:- V_s I_s = 100 W, 

              V_p = 220 V,

              I_p  = 0.5 A

 $$\begin{gathered} \mathrm{\eta } = \frac{100}{220 \times 0.5 } \\ = 0.90 \\ \mathrm{\eta } = 90\% \end{gathered}$$

B.

0.1 s

The current at any instant is given by

I = I_o ( 1 - e^{-R t /L} )

$$\begin{gathered} \frac{{\mathrm{I}}_{\mathrm{o}}}{2} = {\mathrm{I}}_{\mathrm{o}} \left(1 - {\mathrm{e}}^{\raisebox{1ex}{$-\mathrm{R} \mathrm{t} $}\!\left/ \!\raisebox{-1ex}{$\mathrm{L}$}\right.}\right) \\ \frac{1}{2} = \left(1 - {\mathrm{e}}^{\raisebox{1ex}{$\mathrm{R} \mathrm{t} $}\!\left/ \!\raisebox{-1ex}{$\mathrm{L}$}\right.}\right) \end{gathered}$$

e^-Rt/L = 1/ 2

$\frac{\mathrm{Rt}}{\mathrm{L}} = \ln 2$ 

$$\begin{gathered} \therefore \mathrm{t} = \frac{\mathrm{L}}{\mathrm{R}} \ln 2 \\ = \frac{300 \times {10}^{-3}}{2} \times 0.693 \\ = 150 \times 0.693 \times {10}^{-3} \\ \therefore \mathrm{t} = 0.10395 \mathrm{s} \\ \Rightarrow \mathrm{t} = 0.1 \mathrm{s} \end{gathered}$$

A.

increases

When the secondary coil circuit is open, the magnetic flux in the core is produced by the primary current only. When the secondary circuit is closed, the currents in the secondary coil also produce the magnetic flux in the core but in opposite direction. This decreases the core flux and hence reduces the back emf produced in the primary coil.
The source emf is now in excess of the back emf, more current is drawn in the primary coil. Hence, the power factor is no longer zero. The power factor has increased or the phase difference is no longer 90°, ie, phase difference has decreased. Thus, dynamic resistance has increased.

C.

35 V

Given:-  $\mathrm{\varphi } = 5 {\mathrm{t}}^3 - 100\mathrm{t} + 300$

             $\mathrm{e} = -\frac{\mathrm{d\varphi }}{\mathrm{dt}}$

                = $- \frac{\mathrm{d}}{\mathrm{dt}}\left(5 {\mathrm{t}}^3 - 100 \mathrm{t} + 300\right)$

                = $- \left(15 {\mathrm{t}}^2 - 100 + 0\right)$

                 = 15 t² + 100

               $\therefore \frac{\mathrm{e}}{\mathrm{t}}= -15 {\left(3\right)}^2 + 100$

                       = -135 + 100

              $\Rightarrow \frac{\mathrm{e}}{\mathrm{t}} = -35 \mathrm{V}$

D.

0.1 A

The magnitude of induced emf in a circuit is equal to the inductance × rate of current change and a circuit has an inductance of one Henry will have one volt induced in the circuit when the circuit changes at a rate of one ampere per second.

When a current in coil changes, it induces a back emf in the same coil. The self-induced emf is given by

Induced emf,

     $\left|\mathrm{e}\right| = \mathrm{L} \frac{\mathrm{di}}{\mathrm{dt}}$

           = $\left(60 \times {10}^{-3}\right) \times \frac{\left(1.5 - 1\right)}{0.1}$

      $\left|\mathrm{e}\right| =$0.3 V

Induced current,

        i = $\frac{\mathrm{e}}{\mathrm{R}}$

           = $\frac{0.3}{3}$

       i  = 0.1 A

D.

0.1 A

When a current in a coil changes, it induces a back emf back emf in the same coil. The self-induced emf is given by

    Induced emf

                  $\left|\mathrm{e}\right| = \mathrm{L} \frac{\mathrm{di}}{\mathrm{dt}}$

                       = $\left(60 \times {10}^{-3 }\right) \times \frac{\left(3.0 - 2.0\right)}{0.2}$

                        = $\frac{60 \times {10}^{-3} \times 1}{0.2}$

                        = 0.3 A

A changing magnetic field through a coil of wire therefore must induce an emf in the coil which in turn causes current to flow.     

     Induced current 

               i  = $\frac{\mathrm{e}}{\mathrm{R}}$

                 = $\frac{0.3}{3}$

             i  = 0.1 A

C.

V_s = 660 V, i_p = 20 A

Given:- P_in = 4.4 kW,

        V_p = 220 V,

        i_s = 5A,

         V_s = ?

We know that

         i_P = $\frac{{\mathrm{P}}_{\mathrm{in}}}{{\mathrm{V}}_{\mathrm{P}}}$

             = $\frac{4.4 \times {10}^3}{220}$

         i_p = 20A

∴  Efficiency, $\mathrm{\eta } = \frac{\mathrm{output} \mathrm{power}}{\mathrm{input} \mathrm{power}}$

Percentage efficiency

            η = $\frac{{\mathrm{P}}_{\mathrm{out}}}{{\mathrm{P}}_{\mathrm{in}}} \times 100$

         75% = 100 × $\frac{{\mathrm{P}}_{\mathrm{out}}}{4.4 \times {10}^3}$

         P_out = $\frac{75 \times 4.4 \times {10}^3}{100}$

                = 3300 W

∴     P_out = V_S. i_S

⇒        V_S = $\frac{3300}{5}$  

 ⇒        V_S = 660 V 

D.

Zero

Flux through surface A

          $\mathrm{\varphi } = \mathrm{E} \times {\mathrm{\pi R}}^2$

          ${\mathrm{\varphi }}_{\mathrm{A}} = \mathrm{E} \times \mathrm{\pi } {\mathrm{R}}^2$

Flux through curved surface

          C = $\int \mathrm{E} . \mathrm{dS}$

            = $\int \mathrm{Eds}$ cos90^o

           C = 0

Total flux through cylinder = ${\mathrm{\varphi }}_{\mathrm{A}} + {\mathrm{\varphi }}_{\mathrm{B}} + {\mathrm{\varphi }}_{\mathrm{C}}$ 

                                       = 0

C.

$\frac{{\mathrm{\mu }}_0 \mathrm{a}}{2\mathrm{\pi }} \ln \left(1 + \frac{\mathrm{a}}{\mathrm{b}}\right)$

Magnetic field due to wire

      B = $\frac{{\mathrm{\mu }}_0}{2\mathrm{\pi x}} .\mathrm{i}$

      dA = a dx

and  d$\mathrm{\varphi }$ = B. dA

On integrating both sides, we get

     $\int \mathrm{d\varphi } = \int \mathrm{B} \mathrm{dA}$

⇒    $\mathrm{\varphi } = \frac{{\mathrm{\mu }}_0 \mathrm{i}}{2\mathrm{\pi }}$${\int }_{\mathrm{b}}^{\mathrm{a}+\mathrm{b}}\frac{\mathrm{a} \mathrm{dx}}{\mathrm{x}}$

          = $\frac{{\mathrm{\mu }}_0 \mathrm{i}}{2\mathrm{\pi }} \mathrm{a} {\left[ \ln \mathrm{x} \right]}_{\mathrm{b}}^{\mathrm{a}+\mathrm{b}}$

           =$\frac{{\mathrm{\mu }}_0 \mathrm{a}}{2 \mathrm{\pi }}$$\mathrm{a} \left[\ln \left(\mathrm{a} + \mathrm{b} \right) - \ln \mathrm{b} \right]$

           = $\frac{{\mathrm{\mu }}_0}{2 \mathrm{\pi }} \ln \left(1 + \frac{\mathrm{a}}{\mathrm{b}}\right)$ 

            = M i

Where M = coefficient of mutual inductance

and     M = $\frac{{\mathrm{\mu }}_0 \mathrm{i}}{2 \mathrm{\pi }} \ln \left(1 + \frac{\mathrm{a}}{\mathrm{b}}\right)$

C.

the total change in magnetic flux

The induced emf is produced due to change in magnetic flux in the coil.

Induced emf is given by

    e = $- \frac{\mathrm{d\varphi }}{\mathrm{dt}}$

As

   i  = $\frac{\mathrm{e}}{\mathrm{R}}$

      = $-\frac{1}{\mathrm{R}} \frac{\mathrm{d\varphi }}{\mathrm{dt}}$

∴ Total charge induced =$\int \mathrm{i} \mathrm{dt}$

                          = $- \int \frac{1}{\mathrm{R}} \frac{\mathrm{d\varphi }}{\mathrm{dt}}$ dt

                          = $- \frac{1}{\mathrm{R}} {\int }_{{\mathrm{\varphi }}_1}^{{\mathrm{\varphi }}_2} \mathrm{d\varphi }$

                           = $\frac{1}{\mathrm{R}} \left({\mathrm{\varphi }}_1 - {\mathrm{\varphi }}_2\right)$

Thus, the induced charge in a conducting loop, moving in a magnetic field depends on the total change in magnetic flux.        

C.

10.18 × 10^-3 V

Change in magnetic field in 10 s = 2.0 T

As 

    ε = $-\frac{ \mathrm{d\varphi }}{\mathrm{dt}}$

         =$- \mathrm{A} \frac{\mathrm{dB}}{\mathrm{dt}}$                        ( $\because$ $\mathrm{\varphi }$ = BA )

Circumference of patient's trunk 

        2 $\mathrm{\pi }$r = 0.8 m              (given)

∴            r = $\frac{0.8}{2\mathrm{\pi }}$ m

              r = $\frac{0.4}{\mathrm{\pi }}$m

Area of cross section 

              A = $\mathrm{\pi } {\mathrm{r}}^2$

              A = $\mathrm{\pi } {\left(\frac{0.4}{\mathrm{\pi }}\right)}^2$

               A = $\frac{0.16}{\mathrm{\pi }}$m²

∴           $\left|\mathrm{\epsilon }\right| = \frac{0.16}{\mathrm{\pi }} \times \frac{2}{10}$ V

             $\left|\mathrm{\epsilon }\right|$  ≈ 10.18 × 10^-3 V

A.

2 × 10^-5 Wb

Number of turns N = 400

L = 10 mH = 10 × 10^-3 H

I = 2 mA = 2 × 10^-3 A

Total magnetic flux linked with the coil,

 $\mathrm{\varphi }$ = N L I

     = 400 × ( 10 × 10^-3 ) × 2 × 10^-3

$\mathrm{\varphi }$ = 8 × 10^-3 Wb

Magnetic flux through the cross-section of the coil = Magnetic flux linked with each turn

                $= \frac{\mathrm{\varphi }}{\mathrm{N}}$

                = $\frac{8 \times {10}^{-3}}{400}$

                  = 2 ×  10^-5 Wb

D.

7.54 × 10² m

   L = 8 μH = 8 × 10^-6 H

   C = 0.02 μF = 0.02 × 10^-6 F

∴    Resonant frequency

     f_r = $\frac{1}{2\mathrm{\pi } \sqrt{\mathrm{LC}}}$

        = $\frac{1}{2 \mathrm{\pi } \sqrt{8 \times {10}^{-6} \times 0.02 \times {10}^{-6}}}$   

    f_r = 3.98 × 10⁵ Hz

If c ( = 3 × 10⁸ m s^-1 ) is the velocity of the electromagnetic wave, then

Wavelength

      λ = $\frac{\mathrm{c}}{\mathrm{f}}$

          = $\frac{3 \times {10}^8}{3.98 \times {10}^5}$

     λ = 7.54 × 10² m

A.

If both assertion and reason are true and reason is the correct explanation of assertion.

We know

            ε = $\oint \overline{\mathrm{E}} · \overline{\mathrm{dl}}$

               = $-\frac{{\mathrm{d\varphi }}_{\mathrm{B}}}{\mathrm{dt}}$

As          $\oint \overline{\mathrm{E}} · \overline{\mathrm{dl}}$ ≠ 0

the induced electric field is non-conservative in nature.