Sponsor Area
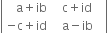
Consider 
= (a + i b) (a - i b)-(c + i b)(- c + i d)
= (a2 - i2 b2 ) - (i2 d2 - c2)
= (a2 + b2 ) - (- d2 - c2) [ 
i2 = - 1 ]
= (a2 + b2 + c2 + d2)
Find the value of each of the following :
(i) sin (sin–1x + cos–1.x) (ii) cos (sec–1x + cosec–1x). | x | ≥ 1
(i) sin (sin–1x + cos–1.x) = 
Sponsor Area
Let y == cosec-1(2) where 
cosec y = 2 where 
required prinicipal value = 
Let y = tan-1(- 1) where 
tan y = -1 where 
required principal value = 
Let y = 
where 0 < y < 
cot y=
where 0 < y < 
requiredf principal value = 
sin[ tan-1 (- 1) ] is a number lying between 
[ by definition ]
and tan x = -1 when x = 
Now sin [ tan-1 (- 1) = sin 
Let sin-1 x=
[ + ve sign taken before square root]
Again, let cos –1x = ϕwhere x ∈ [– 1, 1 ] and ϕ ∈ [0,π]
∴ x = cos ϕ where ϕ ∈ [0, π]
∴sin ϕ is + ve
Sponsor Area
Prove the following :
Put .x = cosθ
∴L.H.S. = 3cos –1(cosθ) = 3 θ
R.H.S. = cos –1(4x3 – 3 x) = cos –1(4 cos3 θ – 3 cos θ)
= cos –1(cos 3 θ) = 3 θ
∴L.H.S. = R.H.S.
Prove the following :
Put x = sin θ
∴L.H.S. = 3 sin –1x = 3 sin–1(sin θ) = 3 θ
R.H.S. = sin–1(3 x – 4 x3)
= sin–1(3 sin θ – 4 sin3 θ)
= sin–1(sin 3 θ) = 3 θ
∴L.H.S. = R.H.S.
Put sin–1.x = θ, sin–1 y = ϕ
∴x = sin θ, y = sin ϕ
Now sin (θ + ϕ) = sin θ cos ϕ + cos θ sinϕ
Prove that 
[ ∵ tan –1 0;≠ 0 as all the terms on L.H.S. are positive and their sum cannot be zero.]
∴ tan –1 1 + tan –1 2 + tan –1 3 = 
From (1) and (2) we get
Now x = – 1 does not satisfy the given equation as the L.H.S. of the equation becomes negative
is the only solution of the given equation.
x + y = - z or x + y = 
x + y + z = 
Sponsor Area
, prove that x + y + z = x y z.
cos–1 x + cos–1y+ cos–1z = π
⇒ cos–1x + cos–1y = π – cos–1z
We are given that
sin–1x + sin–1 y+sin–1z = π
Put x = sin A,y = sin B, z = sin C
∴ sin x = A, sin–1 y = B, sin–1z = C
∴ we have
A + B + C = 
If a line makes angles 90° and 60° respectively with the positive directions of x and y axes, find the angle which it makes with the positive direction of the z-axis.
suppose the direction cosines of the line be l,m,and n.
we know that l2 + m2+n2 = 1
Let the line make angle θ with the positive direction of the z-axis.
α = 90°, β = 60° γ = θ
Thus,
cos2 90 + cos260 + cos2θ =1
Evaluate:
We know that domain and range of the principal value branch of function sin-1 is defined as:
Sponsor Area
Solve for x:
Therefore, x= -1 is not the solution.
When substituting x = in 3x 2x, we have,
Hence x = is the solution of the given equation.
A value of θ for which 
is purely imaginary is
π/3
π/6
D.
Let z = 
is purely imaginary. Then, we have Re (z) = 0
We have Re (z) = 0
Now, consider z = 
If A = sin2 x + cos4 x, then for all real x
3/4 ≤ A ≤ 1
31/16 ≤ A ≤ 1
1≤ A ≤2
3/4 ≤ A ≤ 13/16
A.
3/4 ≤ A ≤ 1
A = sin2x + cos4x = sin2x + (1 - sin2 x)
2 = sin4x - sin2x + 1
then x is equal to
0
C.
0
Here sin-1(1 - x)-2 sin-1 x=
But 
does not satisfy the given equation.
Sponsor Area
Sponsor Area
= (2) (2) - (4) (- 1) = 4 + 4 = 8
=(2) (- 1) - (4) (- 5) = - 2 + 20 = 18
.
required principal value = 
required principal value = 
required principal value = 
required principal value = 
.
required principal value = 
required principal value = 
required principal value = 
required principal value = 
tan y = 1 where 
(B) 
(D) 
is equal
(B) 
(C) 
(D) 
then find the value of x.
, cos-1y=
x=cos 
, y=cos 
in the simplest form.
in the simplest form.
.
is equal to
is equal to
is equal to
find the value of x.
. A normal to y = f (x) at x = π/6 also passes through the point
is equal to
where 
.Then, a value of y is
, is onto, then the interval of S is
