Sponsor Area
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically.
Let present age of Aftab be x years and present age of his daughter be y years.
Case I. Seven years ago,
Age of Aftab = (x - 7) years
Age of his daughter = (y - 7) years
According to question :
(x - 7) = 7 (y - 7)
⇒ x - 7 = 7y - 49
⇒ x - 7y = -42
Case II.
Three years later,
Age of Aftab = (x + 3) years
Age of his daughter = (y + 3) years
Accoring to questions,
x + 3 = 3 (y + 3)
⇒ x + 3 = 3y + 9
⇒ x — 3y = 6
So, algebraic expression be
x - 7y = -42 ...(i)
x - 3y = 6 ...(ii)
Graphical representation
For eq. (i), we have
x - 7y = -42
⇒ x — 7y — 42
Thus, we have following table :
From eqn. (ii), we have
x -3y = 6
⇒ x = 3y + 6
Thus, we have following table
When we plot the graph of equations. We find that both the lines intersect at the point (42, 12). Therefore, x = 42, y = 12 is the solution of the given system of equations.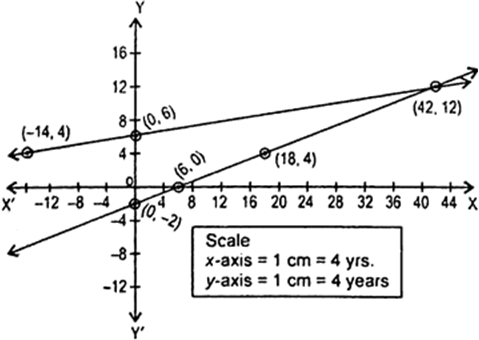
Fig. 3.1.
Let the cost of 1 bat be Rs. x and cost of I ball be Rs.y
Case I. Cost of 3 bats = 3x
Cost of 6 balls = 6y
According to question,
3x + 6y = 3900
Case II. Cost of I bat = x
Cost of 3 more balls = 3y
According to question,
x + 3y = 1300
So, algebraically representation be
3x + 6y = 3900
x + 3y = 1300
Graphical representation :
We have, 3x + 6y = 3900
⇒ 3(x + 2y) = 3900
⇒ x + 2y = 1300
⇒ a = 1300 - 2y
Thus, we have following table :
We have, x + 3y = 1300
⇒ x = 1300 - 3y
Thus, we have following table :
When we plot the graph of equations, we find that both the lines intersect at the point (1300. 0). Therefore, a = 1300, y = 0 is the solution of the given system of equations.
Let the cost of 1 kg of apples be Rs. x and of 1 kg of grapes be Rs. y. So, algebraic representation
<>2x + y = 160
4x + 2y = 300
⇒ 2x + y = 150
Graphical representation, we have
2x + y = 160
⇒ y = 160 - 2x
We have,
2x + y = 150
⇒ y = 150 - 2x
When we plot the graph of the equation we find that two lines do not intersect i.e. they are parallel.
Fig. 3.3.
(i) 10 students of Class X took part in Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(i) Let the number of boys be x and number of girls be y.
Case I. x + y = 10 ...(i)
Case II. y = x + 4
⇒ x - y = -4 ...(ii)
We have, x + y = 10
⇒ x = 10 - y
Thus, we have following table :
Fig. 3.4.
We have, x - y = -4
⇒ x = y - 4
Thus we have following table :
When we plot the graph of the given equation, we find that both the lines intersect at me point (3, 7). So.r = 3,y = 7 is the required solution of the pair of linear equation.
Hence, the number of boys be 3 and the number of girls be 7, who took part in quiz.
Let cost of 1 pencil be Rs. ,v and cost of 1 pen be Rs. y
Case I. Cost of 5 pencils = 5x
Cost of 7 pens = 7y
<>According to question,
5x + 7y = 50
Case II. Cost of 7 pencils = 7x
Cost of 5 pens = 5y
According to question,
7x + 5y = 46
Thus, we have
Thus, we have following table :
Fig. 3.5.
When we plot the graph of the given equation, we find that both the lines intersect at the point (3, 5). So, x = 3,y = 5 is the required solution of the pair of linear equation.
Hence, the cost of 1 pencil be Rs. 3 cost of 1 pen be Rs. 5.
and without drawing them, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincide.
and without drawing them, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincide.
and without drawing them, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincide.
find out whether the following pair of linear equations are consistent, or inconsistent.3x + 2y = 5 ; 2x - 3y = 7
Hence, the given lines are intersecting. So, the given pair of linear equations has exactly one solution and therefore it is consistent.
find out whether the following pair of linear equations are consistent, or inconsistent.2x - 3y = 8; 4x - 6y = 9
Hence, the given lines are parallel. So, the given pair of linear equation it has no solution and therefore it is inconsistent.
find out whether the following pair of linear equations are consistent, or inconsistent.
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041513-3.png)
find out whether the following pair of linear equations are consistent, or inconsistent. 5x-3y=11 ; -10x + 6y = -22
Hence, the given lines are consistent. So, the given pair of linear equations has infinitely many solutions and therefore it is consistent.
find out whether the following pair of linear equations are consistent, or inconsistent.
(i) We have,
x + y = 5 ...(i)
⇒ y = 5 - x
Thus, we have following table
2x + 2y = 10 ...(ii)
Thus, we have following table
When we plot the the graph of the equations we find that both the lines are coincident.
Hence, pair of linear equations has infinitely many solutions
x - y = 8
⇒ y = x - 8
Thus we have following table
Thus, we have following table :
When we plot the graph of the equations. We find the both the lines never meet.
Hence, lines are parallel and equation has no solution.
We have,
2x + y - 6 = 0
⇒ y = 6 - 2x
and 4x - 2y - 4 = 0
⇒ y = 2x - 2
Thus we have following table
When we plot the graph of the equations, we find that both the lines intersect at point (2, 2).
Hence the solution of the given equation is x = 2, y = 2.
Fig. 3.8.
Therefore, the pair of equation is consistent at point (2, 2).
2x - 2y - 2 = 0
⇒ y = x - 1
Thus we have following tables
4x -4y - 5 = 0
When we plot graph of the given equations, we find that both the lines never meet.
Hence lines are parallel and equations has no solutions.
Fig. 3.9.
Sponsor Area
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Let the length of the garden be x m and width bey m.
Case I. x = y + 4
⇒ x - y = 4
Case II.
Half perimeter = 36
⇒ x + y =36
So algebraic representation be
x - y = 4
x + y = 36
Graphical representation :
We have, x - y = 4
⇒ x = 4 + y
Thus, we have following table
x + y = 36
⇒ x = 36 - y
Thus, we have following table :
Fig. 3.10.
If we plot the graph of both the equations, we find that the two lines intersect at the point (20, 16). So, x = 20, y = 16 is the required solution of the given equation i.e., the length of the garden is 20 m and breadth be 16 m.
Given the linear equations 2x + 3y - 8 = 0, write another linear equation in two variables such that the geometrical representing of the pair so formed is :
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines.
We have,
2x + 3y - 8 = 0
(i) Another linear equation in two variables such that the geometrical representation of the pair so formed is intersecting lines is
3x - 2y - 8 = 0
(ii) Another parallel lines to above line is
4x + 6y - 22 = 0
(iii) Another coincident line to above line is
6x + 9y-24 = 0. Ans.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
We have,
x - y + 1 = 0
⇒ y = x + 1
Thus, we have following table :
We have,
3x + 2y-12 = 0
Thus, we have following table :
Fig. 3.11.
When we plot the graph of the given equations, we find that both the lines intersect at the point (2, 3), therefore x = 2, y = 3 is the solution of the given system of equations.
Vertices of triangle (-1, 0) and (4, 0).
C.
Passes through the origin(i) x + y = 14
x - y = 4
The given pair of linear equations is
x + y = 14 ...(i)
x - y = 4 ...(ii)
From equation (i), we have
y = 14 - x ...(iii)
Substitute this value ot’y in equation (ii), we get
x - (14 - x) = 4![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041550-4.png)
Substituting this value of jc in equation (iii), we get
y = 14 - 9 = 5
Therefore the solution is
x = 9, y = 5
Verification. Substituting x = 9 and y = 5. we find that both the equations (i) and (ii) are satisfied as shown below
x + y = 9 + 5 = 14
x - y = 9 - 5 = 4
This verifies the solution.
Solve the following pair of linear equations by the substitution method
s - t = 3
We have
s - t = 3
and ![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041556-6.png)
The given pair of linear equation is
s - t = 3 ...(i)
2s + 3t = 36 ...(ii)
From equation (i), we have
s = 3 + t ...(iii)
Substitute this value of s in equation (ii), we get
2s + 3t = 36
⇐ 2(3 + t) + 3t = 36
⇒ 6 + 2t + 3t = 36
⇒ 5t + 6 = 36
⇒ 5t = 30
⇒ t = 6
Therefore, the solution is
s = 9, t =6
This verifies the solution.
Solve the following pairs of linear equations by the substitution method.
3x – y = 3
9x – 3y = 9
3x – y = 3
9x – 3y = 9
The given pair of linear equation is
3x - y = 3 ...(i)
9x - 3y = 9 ...(ii)
From eqn. (i), we have
y = 3x - 3 ...(iii)
Substitute this value ofy in eq. (ii) we get
9x - 3(3x - 3) = 9
⇒ 9a - 9x + 9 = 9
⇒ 9 = 9
which is true. Therefore eqn. (i) and (ii) have infinitely many solutions.
Solve the following pairs of linear equations by the substitution method.
0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
The given system of linear equations
0.2x + 0.3y = 1.3 ...(i)
0.4x + 0.5y = 2.3 ...(ii)
From equation (i), we have
0.3y =1.3 - 0.2x
Substituting this value ofy in eqn. (ii) we get
0.4x + 0.5 
Substituting this value of x in eqn. (iii), we get
Therefore, the solution is x = 2, y = 3,
Verification. Substituting x = 2 and y = 3, we find that both the equations (i) and (ii) are satisfied as shown below :
0.2a + 0.3y = (0.2) (2) + (0.3) (3)
= 0.4 + 0.9 = 1.3
0.4x + 0.5y = (0.4) (2) + (0.5) (3)
= 0.8 + 1.5 = 2.23
This verifies the solution.
Sponsor Area
Solve the following pairs of linear equations by the substitution method.
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041564-2.png)
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041564-3.png)
Therefore, the solution is
x = 0, y = 0
Verification. Substituting x = 0 and y = 0, we find that both the equation (i) and (ii) are satisfied as shown below :
This verifies the solution.
Solve the following pairs of linear equations by the substitution method.
We have![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041566-2.png)
The given pair of linear equation is
9x - 10y = - 12 ...(i)
2x - 3y = 13 ...(ii)
From (ii), we have
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041566-3.png)
Substituting the value of x in (i), we get
9x - 10y = - 12
Therefore, the solution is
x = 2,y = 3.
Verification. Substituting x = 2 and y = 3, we find that both the equations (i) and (ii) are satisfied as shown below :
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041566-6.png)
Solve 2x + 3y = 11 and 2x – 4y = – 24 and hence find the value of ‘m’ for which y = mx + 3.
The given equations are
2x + 3y = 11 ...(i)
2x - 4y = - 24 ...(ii)
From (i), we have![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041571.png)
Putting the value of ‘x’ in (ii), we get 
Putting the value ofy in (iii), we get
Hence, the solution is x = -2,y = 5.
It is given that: y = mx + 3 Putting the values of.v andy in given condition we gel
5 = m(-2) + 3
⇒ 5 = - 2m + 3
⇒ -2m = 2
⇒ m = -1.
Let the two numbers be x and y
∴ By the given conditions,
x - y = 26 ...(i)
and x = 3y ...(ii)
Substituting x = 3y in (i), we get
3y - y = 26
⇒ 2y = 26
⇒ y = 13
From (ii), x = 3y = 3 × 13 = 39
Thus the numbers are 39 and 13.
Let the larger angle be x and smaller angle bey
According to given conditions,
x + y = 180 ...(i)
and x = y + 18 ...(ii)
Substituting the value of (ii) in (i), we get
x + y = 180
⇒ (y + 18) + y = 180
⇒ y + 18 + y = 180
⇒ 2y = 180 - 18
⇒ 2y = 162
⇒ y = 81° ...(iii)
Putting the value of (iii) in (ii)
x = y + 18
= 81 + 18 = 99°
Thus, the angles arc 81° and 99°.
Form the pair of linear equations for the following problems and find their solution by substitution method.
The coach of a cricket team buys 7 bats and 6 balls for ` 3800. Later, she buys 3 bats and 5 balls for ` 1750. Find the cost of each bat and each ball.
Let the cost of each bat and each ball be Rs. x and Rs. y respectively.
According to given conditions,
7x + 6y = 3800 ...(i)
3x + 5y = 1750 ...(ii)
From eqn. (ii), we get
3x + 5y = = 1750
Substitute the value of eqn. (iii) in (i), we get
7x + 6y = 3800
Substituting the value of x in {iii) we get,![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041585-2.png)
Hence, the cost of one bat = Rs. 500 and cost of one ball = Rs. 50.
Form the pair of linear equations for the following problems and find their solution by substitution method.
The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ` 105 and for a journey of 15 km, the charge paid is ` 155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?
Let fixed charge be Rs. x and charge per km be Rs. y
According to the given conditions,
x + 10y = 105 ...(i)
and x + 15y = 155 ...(ii)
Subtracting (i) from (ii), we get
(x + 15y)-(x + 10y) = 155 - 105
⇒ x + 15y - x — 10y = 50
⇒ 5y = 50 ⇒ y = 10
Putting the value ofy in (i), we get
x + 10y = 105
⇒ x + 10(10) = 105
⇒ x + 100 = 105 ⇒ x = 5
∴ Fixed charge (x) = Rs. 5
and charges per km (y) = Rs. 10
Thus, charges for 25 km
= x + 25y = 5 + 25(10)
= 5 + 250 = Rs. 255.
Form the pair of linear equations for the following problems and find their solution by substitution method.
A fraction becomes 
, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 
. Find the fraction.
Thus, we have following equations
11x - 9y = -4 ...(i)
6x - 5y = -3 ...(ii)
From (ii), we have
6x - 5y=-3
Substituting the value of (iii) in (i), we get
Now, substituting the value ofy in (iii), we get
Hence, the required fraction.
Form the pair of linear equations for the following problems and find their solution by substitution method.
Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
Let the present age of Jacob = x years and present age of his son = y years.
Case I.
5 years hence.
Age of Jacob = (x + 5) yearsand age of his son = (y + 5) years
According to given conditions,
x + 5 = 3 3(y + 5)
⇒ x + 5 = 3y + 15
⇒ x - 3y = 10
Case II.
5 years ago,
Age of Jacob = (x - 5) years and age of his son = (y - 5) years
According to given conditions,
x - 5 = 7(y - 5)
⇒ x - 5 = 7y - 35
⇒ x - 7y = -35 + 5
⇒ x - 7y = -30
Thus, we have following equations
x - 3y = 10 ...(i)
x - 7y = -30 ...(ii)
From (i), we have
x - 3y = 10
⇒ x = 3y + 10 ...{iii)
Substituting the value ofx in (ii), we get
x - 7y = -30
⇒ 3y + 10 - 7y = -30
⇒ -4y + 10 = -30
⇒ -4y = -40
⇒ y = 10
Now, substituting the value of y in (iii), we get
x = 3y + 10
= 3(10) + 10
= 30+10 = 40
Hence,
Age of Jacob = 40 years
and Age of his son = 10 years.
Solve the following pair of linear equations by the elimination method and the substitution method
x + y = 5 and 2x - 3y = 4
x + y = 5 ...(i)
2x - 3y = 4 ...(ii)
For making the cocfficient of y in (i) and (ii) equal, we multiply (i) by 3 and adding, we get
Now, putting the value of x in equation (i), we get
x + y = 5![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041603-1.png)
Hence, 
Substitution method :
We have following equations :
x + y = 5 ...(i)
2x - 3y = 4 ...(ii)
From (i), we have
x + y = 5
⇒ x = 5 -y ...(iii)
Substituting the value ofx in (ii), we get
2x - 3y = 4
2(5 -y)-3y = 4
10 - 2y -3y = 4
10 - 5y = 4
-5y = 4 - 10
-5y = -6
Substitution method :
We have following equations :
x + y = 5 ...(i)
2x - 3y = 4 ...(ii)
From (i), we have
x + y = 5
⇒ x = 5 -y ...(iii)
Substituting the value ofx in (ii), we get
x = 5 - y
Verify that the following system of equations has a unique solution and find the solution
ax + by + m = 0; ax - cy - n = 0
Solution not provided
Ans. 
Solution not provided
Ans. Rs. 1.50
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041615.png)
Solution not provided.
Ans x = 2, y = 1
Solution not provided.
Ans 26 years, 24 years OR 
Solve the following system of linear equations
2(ax - by) + (a + 4b) = 0; 2(bx + ay) + (b - 4a) = 0.
Solution not provided.
Ans. 
Find the value of‘a’ and ‘b’ for which the following system of linear equations has infinite number of solutions :
2x - 3b = 7; (a + b)x - (a + b - 3)y = 4a + b.
Solution not provided.
Ans. a = 5, b = 1
Solution not provided.
Ans. 21 Yrs., 27 yrs.
Solution not provided.
Latakshi started her job in the begining of year 1991 with a slary of Rs. x per month and earned an yearly increment of Rs. y, if her salary at the begining of year 1996 was Rs. 3,000 and at the begining of year 2000 was Rs. 4,200; find
(i) the values of x and y. (ii) Latakshi’s monthly salary during 1994 and during 1999.
Solution not provided.
Ans. (i) x = 1500, y = 300, (ii) Rs. 2400 and Rs. 3900
Solution not provided.
Ans. 6l, 15l
Solution not provided.
Ans. A(0,0) B (25,4), C(3,3)
Draw the graphs of the following equations on the same graph paper. 2x + 3y = 12, x - y = 1 .
Find the co-ordinates of the vertices of the triangle formed by the two straight lines and the y-axis.
Solution not provided.
Ans. A(0,4) B (3,2), C(0,-1)
Solution not provided.
Ans. k = 5
Solution not provided.
Ans. p = 5, q = 1
Solution not provided
Ans. k = 1
Solution not provided.
Ans. 64
Solution not provided.
Ans. 7.5 sq. units
Solution not provided.
Ans. 12 sq. units
Sponsor Area
Solution not provided.
Ans. 8 sq. units
Solution not provided.
Ans. a = -5, b = -1
Solution not provided.
Ans. 60km/hr, 40km/hr
Solution not provided.
Ans. 36 or 63
Solve the following system of linear equations graphically: 2x - 3y = 1, 3x - 4y = 1 Does the point (3,2) lie on any of the lines? Write its equation.
Solution not provided.
Ans. Yes, 3x - 4y = 1
Solve the following system of linear equation graphically: 3x - 5y = 19, 3y - 7x - 1 = 0. Does the point (4, 9) lie on any of the lines? Write its equaiton.
Solution not provided.
Ans. Yes, 3x - 7y + 1 = 0
Solution not provided.
Ans. a = - 6
Solution not provided.
Ans. a = 2, b =3
Solution not provided.
Ans. A(0,3), B(0,5), C(0, -4)
Solve the following system of linear equation graphically: 5x - 67 - 30 = 0, 5x + 4y - 20 = 0. Find the vertices of the triangle formed by the above two lines, and x-axis.
Solution not provided.
Ans. A(-6,0), B(0, 5), C(4, 0)
Solution not provided.![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041667.png)
For what values of a and b does the following pair of linear equations have an enfinitc no. of solution :
2x + 3y = 7
a (x + y) -b (x - y) = 3a + b - 2
Solution not provided.
Ans. a = 5, b =1
Solution not provided.
Ans. x = 4, y =5
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041678.png)
Solution not provided.
Ans. x = 8, y = 3
Represent the following pair of equations graphically and write the co-ordinates of pairs where the lines intersect y-axis.
x + 3y = 6; 2x - 3y = 12
Solution not provided.
Ans. (6, 0)
Find the number of solutions of the following pair of linear equations :
x + 2y - 8 = 0; 2x + 4y = 16
Solution not provided.
Ans. Infinite many solution.
Find the values of k for which the pair of equations :
kx + 3y = k - 2 and 12x + ky = k has no solution.
Solution not provided.
Ans. 
Solution not provided.
Ans. 60 km/hr, 40 km/hr
Solution not provided.
Ans. Consistent
Solution not provided.
Ans. Lines are parallel.
Solution not provided.
Ans. Unique Solution.
Let the cost of 1 bat be Rs. x and cost of I ball be Rs.y
Case I. Cost of 3 bats = 3x
Cost of 6 balls = 6y
According to question,
3x + 6y = 3900
Case II. Cost of I bat = x
Cost of 3 more balls = 3y
According to question,
x + 3y = 1300
So, algebraically representation be
3x + 6y = 3900
x + 3y = 1300
Graphical representation :
We have, 3x + 6y = 3900
⇒ 3(x + 2y) = 3900
⇒ x + 2y = 1300
⇒ a = 1300 - 2y
Thus, we have following table :
We have, x + 3y = 1300
⇒ x = 1300 - 3y
Thus, we have following table :
When we plot the graph of equations, we find that both the lines intersect at the point (1300. 0). Therefore, a = 1300, y = 0 is the solution of the given system of equations.
Verify that the following system of equations has a unique solution and find the solution
ax + by + m = 0; ax - cy - n = 0
Solution not provided.
Ans. 
Solution not provided.
For what values of a and b does the following pair of linear equations have an enfinitc no. of solution :
2x + 3y = 7
a (x + y) -b (x - y) = 3a + b - 2
Solution not provided.
Ans. a = 5, b = 1
Solve the following pair of linear equations by the elimination method and the substitution method
x + y = 5 and 2x – 3y = 4
Elimination Method :
(i) x + y = 5 ...(i)
2x - 3y = 4 ...(ii)
For making the cocfficient of y in (i) and (ii) equal, we multiply (i) by 3 and adding, we get
Now, putting the value ofx in (i), we get
3x + 4y = 10
⇒ 3(2) + 4y = 10
⇒ 6 + 4y = 10
⇒ 4y = 4
⇒ y = 1
Hence, x = 2, y = 1
Substitution method :
We have,
3x + 4y = 10 ...(i)
2x - 2y = 2 ...(ii)
From (i), we have
Now, putting the value of x in equation (i), we get
x + y = 5
Now, putting the value of x in equation (i), we get
x + y = 5
Substituting the value ofx in (ii), we get
2x - 3y = 4
Solve the following pair of linear equations by the elimination method and the substitution method
3x + 4y = 10 and 2x – 2y = 2
3x + 4y = 10 ...(i)
2x - 2y = 2 ...(ii)
For making the coefficient of y in (i) and (ii) equal, we multiply (ii) by 2 and adding we get.
Now, putting the value ofx in (i), we get
3x + 4y = 10
⇒ 3(2) + 4y = 10
⇒ 6 + 4y = 10
⇒ 4y = 4
⇒ y = 1
Hence, x = 2, y = 1
Substitution method :
We have,
3x + 4y = 10 ...(i)
2x - 2y = 2 ...(ii)
From (i), we have
3x + 3y = 10![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041739-1.png)
Substituting the value of (iii) in (ii), we get
2x - 2y = 2
Now, substituting the value ofy in (iii), we get
Hence, x=2, y=1
Solve the following pair of linear equations by the elimination method and the substitution method
3x – 5y – 4 = 0 and 9x = 2y + 7
3x - 5y = 4 ...(i)
9x - 2y = 7 ...(ii)
For making the coefficient of x in (i) and (ii) equal, we multiply eqn. (i) by 3 and subtracting, we get
9x - 15y = 12
9x - 2y = 7
- + -
-13y = 5
Now putting the value of y in (i), we get
Substitution method :
We have,
3x - 5y = 4 ...(i)
9x - 2y = 7 ...(ii)
From (i), we have
3x - 5y = 4
Substituting the value of (iii) in (ii), we get
Now, substituting the value ofy in (iii), we get
Solve the following pair of linear equations by the elimination method and the substitution method![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041749.png)
Now, we have following pairs of equations
3x + 4y = - 6 ...(i)
3x -y = 9 ...(ii)
Since the coefficients of ‘x’ in (i) and (ii) are equal. So simply by subtracting we can eliminate the variable i.e., x.
Now putting the value ofy in eqn. (i), we get
3x + 4y = - 6
3x + 4(-3) = - 6
⇒ 3x - 12 = -6
⇒ 3x = 6
⇒ x = 2
Hence, x = 2, y = -3.
Substitution method :
We have,
Now, we have following pairs of equations
3x + 4y = -6 ...(i)
3x - y = 9 ...(ii)
From (ii), we have
3x - y = 9
⇒ y = 3x - 9 ...(iii)
Substituting the value of (iii) in (i), we get
3x + 4y = -6
⇒ 3x + 4(3x - 9) = -6
⇒ 3x + 12x - 36 = -6
⇒ 15x = -6 + 36
⇒ 15x = 30
⇒ x = 2
Now, substituting the value ofx in (iii), we get
y = 3x - 9
= 3(2) - 9 = 6 - 9= -3
Hence, x = 2, y = -3.
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :
If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to It becomes 
if we only add I to the denominator. What is the fraction?
Thus, we have following equation
x - y = -2 ...(i)
2x - y = 1 ...(ii)
From (i), we have
x - y = -2
⇒ x = y - 2 ...(iii)
Substituting the value of x in (ii), we get
2x - y = 1
⇒ 2(y - 2) - y = 1
⇒ 2y - 4 - y = 1
⇒ y - 4 = 1⇒ >> y = 5
Now, substituting the value ofy in (iii), we get
x = y - 2
= 5 - 2 = 3
Hence, the required fraction 
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :
Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
Let the present age of Nuri be x years and present age of Sonu be y years.
Case I.
5 years ago,
Age of Nuri = (x - 5) years
and Age of Sonu = (y - 5) years
According to the given conditions,
x - 5 = 3(y - 5)
⇒ x - 5 = 3y - 15
⇒ x - 3y = -10
Case II.
Ten years later,
Age of Nuri = (x + 10) years
Age of Sonu = (y + 10) years
According to the given conditions,
x + 10 = 2(y + 10)
⇒ x + 10 = 2y + 20
⇒ x - 2y = 10
Thus, we have following equations :
x - 3 y = -10 ...(i)
x - 2y = 10 ...(ii)
From (i), we have
x - 3y = -10
⇒ x = 3y - 10 ...(iii)
Substituting the value of (iii) in (ii), we get
x - 2y = 10
⇒ 3y - 10 - 2y = 10
⇒ y = 20
Now, substituting the value ofy in (iii), we get
x = 3y - 10
= 3(20)- 10
= 60 - 10 = 50
Hence, Age of Nuri = 50 years
and Age of Sonu = 20 years.
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :
The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Let the digit at Unit’s place be x and digit at ten’s place be y
Then,the number= 10y + x
Also, the number obtained by reversing the order of the digits = 10x + y
According to the given condition,
x + y = 9 ...(i)
And 9(10y + x) = 2(10x + y)
⇒ 90y + 9x = 20x + 2y
⇒ 11x - 88y = 0
⇒ x - 8y = 0 ...(ii)
Subtracting equation (ii) from equation (i), we get
9y = 9
Substituting this value ofy in equation (i), we get
x + 1 = 9
⇒ x = 9 - 1 = 8
Hence, the required number
= 10y + x
= 10(1)+ 8
= 10 + 8 = 18.
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :
Meena went to a bank to withdraw ` 2000. She asked the cashier to give her ` 50 and ` 100 notes only. Meena got 25 notes in all. Find how many notes of ` 50 and ` 100 she received.
Suppose that Meena received x notes of Rs. 50 andy notes Rs. 100.
Then, according to the given conditions
x + y = 25 ...(i)
And 50x + 100y = 2000
⇒ x + 2y = 40 ...(ii)
Subtracting equation (i) from equation (ii), we get
y = 15
Substituting this value of y in equation (i), we get
x + 15 = 25
⇒ x = 25 - 15 = 10
Hence, Meena received 10 notes of Rs. 50 and 15 notes of Rs. 100
Sponsor Area
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ` 27 for a book kept for seven days, while Susy paid ` 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Let the fixed charge be Rs. a and the charge for each extra day be Rs. b.
Then, according to the given conditions,
a + 4b = 27 ...(i)
[Extra days = 7 - 3 = 4]
a + 2b = 21 ...(ii)
[Extra days = 5 - 3 = 2]
Subtracting equation (ii) from equation (i), we get
2b = 6![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041764.png)
Substituting this value of b in equation (ii), we get
a + 2(3) = 21
⇒ a + 6 = 21
⇒ a = 21 - 6 = 15
Hence, the fixed charges one Rs. 15 and the charge for each extra day is Rs. 3.
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
x – 3y – 3 = 0
3x – 9y – 2 = 0
The given pair of linear equation is
x - 3y - 3 = 0
3x - 9y - 2 = 0
Here, a1 = 1, b1 = -3
a2 = 3, b2 = -9, c2= -2
Wee see that![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041767.png)
Hence, the given pair of linear equations has no solutions.
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
2x + y = 5
3x + 2y = 8
2 x + y = 5
3x + 2y = 8
The given pair of linear equations is
2x + y = 5
3x + 2y = 8
⇒ 2x + y - 5 = 0
3x + 2y - 8 = 0
Here, a1 = 2, b1 = 1, c, = -5
a2 = 3, b2 = 2, c2 = -8
We see that,
Hence, the given pair of linear equations has a unique solution.
To solve the given equation by cross multiplication method, we draw the diagram below :
Hence, the required solution of the given pair of linear equation is x = 2, y = 1.
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
3x - 5y = 20
6x - 10y = 40
3x - 5y = 20
6x - 10y = 40
The given pair of linear equations is
3x - 5y = 20
6x - 10y = 40
⇒ 3x - 5y - 20 = 0
6x - 10y - 40 = 0
Here, a1 = 3, b1 = -5, c1 = -20
a2 = 6, b2 10, c2 = —40
We see that
Hence, the given pair of linear equation has infinitely many solution.
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
x - 3y - 7 = 0
3x - 3y - 15 = 0
x - 3y - 7 = 0
3x - 3y - 15 = 0
The given pair of linear equations is
x - 3y - 7 = 0
3x - 3y - 15 = 0
Here, a1 = 1, b2 = -3, c1 = -7
a2 = 3, b2 = -3, c2 = -15
We see that
Hence, the given pair of linear equations has a unique solution.
To solve the given equations by cross multiplication method, we draw the diagram below :
For which values of a and b does the following pair of linear equations have an infinite number of solutions ?
2x + 3y = 7
(a - b) x + (a + b) y = 3a + b - 2
We have following equations
2x + 3y = 7
(a - b)x + (a + b)y = 3a + b - 2>
Here, a1 = 2, b1 = 3, c1 = 7
and a2 = a - b, b2 = a + b,
c2 = 3a + b -2
For having an infinite number of solutions, we must have
From First two.![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041783-1.png)
Thus, we have following equations
a - 5b = 0 (i)
a - 2b - 3 = 0 (ii)
For which value of k will the following pair of linear equations have no solution?
3x + y = 1 (2k – 1) x + (k – 1) y = 2k + 1
The given pair of linear equations is
3x + y = 1
(2k - 1) x + (k - 1) y= 2k + 1
⇒ 3x + y - 1 = 0
Here, (2k - 1) x + (k - 1) y - (2k + 1) = 0
a1 = 3, b1 = 1, c1 = -1)
a2 = 2 k - 1, b2 = k - 1 c2 = - (2k + 1)
For having no solution, we must have![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041784.png)
Solve the following pair of linear equations by the substitution and cross-multiplication methods :
8x + 5y = 9
3x + 2y = 4
The given pair of linear equations is
8x + 5y = 9 ...(i)
3x + 2y = 4 ...(ii)
(I) By substitution method
From equation (ii), we have
2y = 4 - 3x
Substitute this value ofy in equation (i), we get![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041786-1.png)
Substituting this value of x in equation (iii), we get![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041786-2.png)
So, the solution of the given pair of linear equations is x = -2,y = 5.
(II) By cross-multiplication method
Let us write the given pair of linear equations is
8x + 5y - 9 = 0 ...(i)
3x + 2y - 4 = 0 ... (ii)
Solving the equations, we get
Hence, the required solution of the given pair of linear equations is x = -2, y - 5.
(i) Let the fixed hostel charges be Rs. x and the cost of food per day Rs. y (Running charges)
Case I. Hostel charges of ‘A’
Fixed charges be Rs. x and cost of food for 20 days = 20y According to Question,
x + 20y = 1000
Case II. Hostel charges of ‘B’
Fixed charges be Rs. x and cost of food for 26 days = 26y According to question,
x + 26y = 1180
Thus, we have following equations
x + 20y = 1000
x + 2 6y = 1180
or x + 20y - 1000 = 0
x + 26y- 1180 = 0
Now, by using cross multiplication method,
Hence, fixed charges is Rs. 400 and cost of food per day is Rs. 30.
when 1 is subtracted from the numerator and it becomes 
when 8 is added to its denominator. Find the fraction.
Let the number of correct answers of Yash be x and number of wrong answers be y. Then according to question :
Case I. He gets 40 marks if 3 marks are given for correct answer and 1 mark is deduced for incorrect answers.
3x - y = 40
Case II. He gets 50 marks if 4 marks are given for correct answer and 2 marks ar deducted for incorrect answers.
4x - 2y = 50
Thus, we have following equation
3x - y - 40 = 0
4x -2y - 50 = 0
Now, using cross multiplication method,
Hence, total number of questions
= number of correct answers
+ number of incorrect answers
= 15 + 5 = 20.
Let the speed of the car starting from point A be .v km/h and speed of the car starting from point B be y km/hr.
Case I. When they travel in the same direction, let they meet at point P (Fig. 3.12).
So, AP = distance covered by first car from point A to P
= speed x time
= x × 5 = 5
and BP = distance covered by second car from point B to P
= speed × time
= y × 5 = 5y
Therefore, AB = AP - BP
⇒ 100 = 5x - 5y
⇒ 5a - 5y = 100
⇒ x - y = 20
Case II. (Fig. 3.13)
When they travel in opposite direction, let they meet at point Q.
So, AQ = Distance covered by first car from point A to Q
= Speed × Tinte
= x × 1 = x
and BQ = Distance covered by second car from point B to Q
= Speed × Time
= y × 1 = y
Therefore, AB = AQ + BQ
⇒ 100 = x + y
⇒ x + y = 100
Thus, we have following eqn.
x - y = 20
x + y = 100
⇒ x - y - 20 = 0
x + y - 100 = 0
Hence, speed of the car that starts from point A = 60 km/hr
Speed of the car that starts from point B = 40 km/hr.
Let the dimensions (i.e., the length and the breadth) of the rectangle be x units and y units respectively.
Then, area of the rectangle
= length × breadth
= xy square units
According to the question,
xy - 9 = (x - 5) (y + 3)
⇒ xy - 9 = xy + 3x - 5y - 15
⇒ 3x - 5y - 6 = 0
and xy + 67 = (x + 3) (y + 2)
⇒ xy + 67 = xy + 2x + 3y + 6
⇒ 2x + 3y - 61 =0
Thus, we have following equatins
3x - 5y - 6 = 0 (i)
2x + 3y - 61 =0 (ii)
Hence, the dimensions (i.e., the length and the breadth) of the rectangle are 17 units and 9 units respectively.
Thus, we have two equations
3u + 2v = 12 ...(i)
2u + 3v = 13 ...(ii)
From (i), we have
Putting the value of ‘u’ in (ii), we get
Putting the value of ‘v’ in (iii), we get![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041799-5.png)
is the solution of the given equation.
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041802.png)
Then the given system of equation becomes
2u + 3v = 2 ....(i)
4u - 9v = -1 ...(ii)
For making the co-efficients of ‘u’ in (i) and (ii) equal, we multiply (i) by 2 and then subtracting
Thus, the given equations become
4a + 3y = 14 ...(i)
3a - 4y = 23 ...(ii)
For making the coefficient of ‘y’ in (i) and (ii), we multiply (i) by 4 and (ii) by 3 and then adding, we get
, is the solution of the given equation.Solve the following pairs of equations by reducing them to a pair of linear equations:
Thus, the given equations becomes
5u + v = 2 ...(i)
6u - 3v = 1 ...(ii)
For making the coefficient of v in (i) and (ii) equal, we multiply (i) by 3 and adding, we get
Putting the value of u in (i), we get
5u + v = 2
Solve the following pairs of equations by reducing them to a pair of linear equations:
Then the given system of equations become
Solve the following pairs of equations by reducing them to a pair of linear equations:
6x + 3y = 6xy
2x + 4y = 5x
Considering equation
6x + 3y = 6xy
Dividing both side by xy, we get
Considering equation
2x + 4y = 5xy
Dividing both side by xy, we get![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041812-1.png)
The given system of equation becomes
6v + 3u = 6 ....(iii)
2v + 4u = 5 ....(iv)
For making the coefficient of u in (iii) and (iv) equal, we multiply (iii) by 4 and (iv) by 3 and by subtracting, we get
Putting the value of v in (iii), we get
Solve the following pairs of equations by reducing them to a pair of linear equations:
Then the given system of equation becomes
10u + 2v = 4 ...(i)
15u - 5v = -2 ...(ii)
For making the coefficient of v in (i) and (ii) equal, we multiply (i) by 5 and (ii) by 2 and then adding, we get
Putting the value of u in (i), we get
10u + 2v = 4
Substituting the value of x in (iv), we get
x - y = 1
⇒ 5 - y - y = 1
⇒ 5 - 2y = 1
⇒ -2y = 1 - 5 ⇒ -2y = -4
⇒ y = 2
Now, substituting the value of in (v), we get
x = 5 - y
= 5 - 2 = 3
Hence, x = 3, y = 2.
Solve the following pairs of equations by reducing them to a pair of linear equations:
Adding (iii) and (iv), we get
6x = 6
⇒ x = 1
Putting the value of ‘x’ in (iii), we get
3 x + y = 4
⇒ 3(1) + y = 4
⇒ y = 1
Hence, x = 1, y = 1 is the solution of the given equation.
Formulate the following problems as a pair of equations, and hence find their solutions:
Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
Let the speed of the boat in still water = x km/hr
and speed of the current = y km/hr
Now, the speed of the boat upstream = (x - y) km/hr
and the speed of the boat downstream = (x + y) km/hr
Case I. Time taken to cover 20 km downstream
Case II. Time taken to cover 4 km upstream
Putting the value of ‘x’ in (ii), we get
10 - y - y = 2
⇒ 10 - 2y = 2
⇒ -2y = -8
⇒ y = 4
Now, substituting the value ot y in (i), we get
x + y = 10
⇒ x + 4 = 10
⇒ x = 6
Hence, speed of rowing her boat in still water = 6 km/hr
and speed of the current = 4 km/hr.
Formulate the following problems as a pair of equations, and hence find their solutions:
2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
Let 1 woman can finish embroidery work in x days
and 1 man can finish embroidery work in y days
∴ 1 woman’s 1 day’s work 
and 1 man’s 1 day’s work 
Case I. 2 women’s 1 day’s work 
and 5 men’s 1 day’s work ![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041820-12.png)
According to question ![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041820-13.png)
Case II. 3 women’s 1 day’s work ![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041820-14.png)
and 6 men’s 1 day’s work 
According to question 
Taking 
we have
For making the coefficient of ‘u’ we multiply equation (i) by 3 and equation (ii) by ‘2’ and then subtracting, we get
Hence, 1 woman alone can finish the work in 18 days and 1 man alone can finish the work in 36 days.
Formulate the following problems as a pair of equations, and hence find their solutions:
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Let the speed of the train and the bus be x km/hour and y km/hour respectively.
Case I. When she travels 60 km by train and the remaining (300 - 60) km, i.e., 240 km by bus, the time taken is 4 hours.![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041831.png)
Case II. When she travels 100 km by train and the remaining (300 - 100) km, i.e., 200 km by bus.
the time taken is 4 hours 10 minutes, i.e., 
hours.![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041831-2.png)
[Dividing by 25]
Multiplying equation (i) by (ii), we get
Subtracting equation (iii) from equation (ii), we get![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041831-4.png)
Substituting this value of x in equation (iii), we get![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041831-5.png)
So, the solution of the equations (i) and (ii) is x = 60 and y = 80.
Hence, the speed of the train is 60 km/hour and the speed of the bus is 80 km/hour.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Let the ages of Ani and Biju be x years and y years respectively. Then, according to the question,
x - y = ±3 ...(i)
Age of Ani’s father Dharam = 2x years
Age of Biju’s sister 
According to the question,
Case I. When x - y = 3
Then, we have
x - y = 3 ...(i)
4x - y = 60 ...(ii)
Subtracting equation (i) from eq. (ii)![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041832-2.png)
Substituting the vaiue of x in eqn. (i)
19 - y = 3
y = 19 - 3 = 16
Ani’s age = 19 years
Biju’s age = 16 years.
One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II]
Let the amounts of their respective capitals be Rs. x and Rs. y respectively.
Then, according to the question,
x + 100 = 2(y - 100)
⇒ x - 2y = -300 ...(i)
and 6(x - 10) = y + 10
⇒ 6x — y = 70 ...(ii)
From equation (i), we have
x = 2y - 300 ...(iii)
Substitute the value of x in equation (ii), we get
Substituting the value of>> in equation (iii), we get
x = 2(170) - 300
= 340 - 300 = 40
So, the solution of the equations (i) and (ii) is x = 40 and y - 170. Hence, the amounts of their respective capitals are Rs. 40 and Rs. 170 respectively.
A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Let the actual speed of the train be x km/hr and the actual time taken by y hours. Then,
Distance covered = (xy) km ...(i)
Case I. If the speed is increased by 10 km/hr then time of journey is reduced by 2 hrs i.e. when speed is (x + 10) km/hr, time of journey is (y - 2) hrs.
∴ Distance covered = (x + 10) (y - 2)
⇒ xy = xy - 2x + 10y - 20
[Using (i)]
⇒ 2x - 10y = -20
Case II. When the speed is reduced by 10 km/hr then time of journey is by 3 hrs i.e. when speed is (x - 10) km/hr, time of journey is (y + 3) hrs.
∴ Distance covered = (x - 10) (y + 3)
⇒ xy = (x - 10) (y + 3)
[Using (i)]
⇒ xy = xy + 3x - 10y - 30
⇒ -3x + 10y = -30
Thus, we have following eqn.
2x - 10y = -20 ...(i)
-3x + 10y = -30 ...(ii)
Since, the coefficient of y in both the equations are same, so we can eliminate it
directly by adding i.e.![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041834.png)
Putting the value of x in (i), we get
2x - 10y = -20
⇒ 2(50) - 10y = -20
⇒ 100 - 10y = -20
⇒ -10y = -120
⇒ y = 12
Hence, the distance covered by the train
= (xy) km
= (50 × 12) km
= 600 km.
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Let the total no. of students in each row be x and the total no. of rows by y
∴ Total no. of students in the class = xy ...(i)
Case I. If 3 students are extra in a row, there would be 1 row less. i.e.
total no. of students in each row = (a + 3)
and the total no. of rows = (y - 1)
∴ Total no. of students in the class
= (x + 3)(y - 1) ...(ii)
Comparing (i) and (ii), we get
xy = (x + 3) (y - 1)
⇒ xy = xy - x + 3y - 3
⇒ x - 3y = -3
Case II. If 3 students are less in a row, there would be 2 rows more. i.e.
total no. of students in each row = (x - 3)and the total no. of rows = (y + 2)
∴ Total no. of students in the class
= (x - 3)(y + 2) ...(iii)
Comparing (i) and (iii), we get
xy = (x - 3) 0 + 2)
⇒ xy = xy + 2x - 3y - 6
⇒ -2x + 3y = -6
Thus, we have following equations
x - 3y = -3 ...(iv)
-2x + 3y = -6 ...(v)
From (iv), we have
x - 3y = -3
⇒ x = 3y - 3 ...(vi)
Substituting the value of (vi) in (v), we get
-2x + 3y = -6
⇒ -2(3y - 3) + 3y = -6
⇒ -6y + 6 + 3y = -6
⇒ -3y = -12
⇒ y - 4
Now, substituting the value of ‘y’ in (vi), we get
x = 3y - 3
= 3(4) - 3 = 12 - 3 = 9
Hence, total no. of students in the class
= xy
= 9 × 4 = 36.
In a Δ ABC, ∠ C = 3 ∠ B = 2 (∠ A + ∠ B). Find the three angles.
Let ∠A = x°, ∠B = y°. Then,
∠C = 3∠B = ⇒ ∠C = 3y°
We have. ∠C = 3 ∠B = 2 (∠A + ∠B). ...(i)
Now,0 3∠B = 2 (∠A + ∠B) From (i)
⇒ 3y = 2(x + y)
⇒ y = 2x
Since ∠A, ∠B and ∠C are angles of a triangle.
∴ ∠A + ∠B + ∠C = 180°
⇒ x + y + 3y = 180
⇒ x + 4y = 180 ...(ii)
Putting y = 2x in equation (ii), we get
x + 4(2x) = 180
⇒ x + 8x = 180
⇒ 9x = 180
⇒ x = 20°
Putting the value of x equation (i), we get y = 40°
Hence, ∠A = 20°, ∠B = 40°
and ∠C = 3y° = (3 × 40°)= 120°.
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and the y axis.
The given equations are
5x - y = 5 ...(i)
3x - y = 3 ...(ii)
For equation (i), we have
= 5x - 5
Thus, we have following table :
For equation (ii), we have
y = 3x - 3
Thus, we have following table :
Fig. 3.14.
Solve the following pair of linear equations:
px + qy = p - q
qx - py = p + q
we get
Putting the value of ‘x’ in (ii), we get
Putting the value of ‘y’ in (iii), we get
Hence, the solution is
x = 1, y = -1.
Solve the following pair of linear equations:
ax + by = c
bx + ay = 1 + c
We have,
ax + by = c ...(i)
bx + ay = 1 + c ...(ii)
From (i), we have
Putting the value of (iii) in (ii), we get
Putting the value of ‘y’ in (iii), we get
Hence, the solution is
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041845-1.png)
Solve the following pair of linear equations:![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041849.png)
Putting the value of x in (ii), we get
(a + b)x + (a + b) y = a2 + b2
⇒(a + b) (a + b) + (a + b)y = a2 + b2
⇒ (a + b)2 (a + b)y = a2 + b2
⇒(a + b)y = (a2 + b2) - (a + b)2
⇒ (a + b)y = (a2 + b2) - (a2 + b2 + 2ab)
⇒ (a + b)y = a2 + b2 - a2 - b2 - 2ab
⇒ (a + b)y = - 2ab
Hence,
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041849-3.png)
Solve the following pair of linear equations:
152x – 378y = – 74
–378x + 152y = – 604
152x - 378y = -74
-378x + 152y = -604
The given pair of linear equations is
152x - 378y = -74 ...(i)
-378x + 152y = -604 ...(ii)
Adding equation (i) and equation (ii), we get
-226x - 226y = -678
⇒ x + y = 3 ...(iii)
[Dividing throughout by -226]
Subtracting equation (ii) from equation (i), we get
530x - 530y = 530
⇒ x - y = 1 ...(iv)
[Dividing throughout by 530]
Adding equation (iii) and equation (iv), we get
2x = 4
Subtracting equation (iv) from equation (iii), we get
2y = 2
Hence, the solution of the given pair of linear equations is x = 2, y = 1.
ABCD is a cyclic quadrilateral (see Fig. 3.7). Find the angles of the cyclic quadrilateral.
We know that the opposite angles of a cyclic quadrilateral are supplementary, therefore,
∠A + ∠C = 180°
⇒ 4y + 20 + 4x = 480°
⇒ 4x + 4y = 60°
⇒ x + y = 40° ...(i)
[Dividing throughout by 4]
and ∠B + ∠D = 180°
⇒3y - 5 + 7x + 5= 180°
⇒ 7x + 3y = 180° ...(ii)
From equation (i), we have
y = 40 - x ...(iii)
Substituting this value of y in equation (ii), we get
7x + 3(40 - x) = 180°
⇒7x + 120 - 3x = 180°
⇒ 4x = 60
Substituting x = 15 in equation (iii), we get
y = 40 - x
= 40 - 15 = 25°
Hence, required angles be
∠A = 4y + 20 = 4 × 25 + 20 = 120
∠B = 3y - 5 = 3 × 25 - 5 = 75 - 5 = 70
∠C = 4x = 4 × 15 = 60°
∠D = 7x + 5 = 7 × 15 + 5
= 105 + 5 = 110°
Find the number of solutions of the follow ing pair of linear equations :
x + 2y - 8 = 0
2x + 4y = 16
The given pair of linear equations can be written as
x + 2y - 8 = 0
and 2x + 4y - 16 = 0
∴ There are infinitely many solutions.
Is the pair of linear equations consistent:
2x - 3y + 2 = 0,3x - 5y + 4 = 0.
We have
2x - 3y + 2 = 0 and 3x - 5y + 4 = 0
Here, a1 = 2, b1 = -3 and c1 = 2
and a2 = 3, b2 = -5 and c2 = 4
Conditions for consistency :
So, the pair of linear equation are consistent.
We have,
Here, a1 = 3, b1 = -1 and c1 = -5
and a2 = 6, b2 = -2 and c2 = -k
For no solution, we have
Hence the given system, we have no solution if k = 10.
Given pair of linear equations are :
3x - ky + 7 = 0
and x - 2y + 5 = 0
Here, we have
a1 = 3, b1 = -k
a2 = 1, b22 = -2
For unique solution![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041872.png)
∴ The given system of linear equations has unique solution for all real values of k other than 6.
2x - 3y = 4; 4x - 6y = 7; 6x - 9y - 12.
Sol. Pair of infinite solutions :
2x - 3y = 4; 6x - 9y = 12
Here, a1 = 2, b1 = -3 and c1 = 4
and a2 = 6, b2 = -9 and c2 = 12
The given values satisfy the condition :![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041889.png)
So, given equations have infinite solutions pair of no solutions :
2x - 3y = 4; 4x - 6y = 7
Here, a1 = 2, b1 = -3 and c1 = 4
and a2 = 4, b2 = -6 and c2 = 7
The given values satisfy the condition:![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041889-1.png)
So, given equations have no solutions.
The given pair of equation is
2x + 3y = 5
5x - 2y = 3
Putting x = 1,y = 1 in eq. (i) and (ii), we get
2x + 3y = 5
⇒ 2(1) + 3(1) = 5
⇒ 5 = 5 which is true.
Also, 5a - 2y = 3
⇒ 5(1) - 2(1) = 3
⇒ 3 = 3 which is true.
Thus, x = 1, y - 1 is the solution of the given pair of equations.
Write whether the following pair of linear equations is consistent or not.
x + y = 14
x - y = 4
x + y = 14
x - y = 4
the equation have unique solution.
Pair of linear equations are consistent.
Here, a1 = 3, b1 = -1 and c1 = -5
a2 = 6, b2 = -2 and c2 = k
Hence the given system will have infinite no. of solution if k = -10.
We have,
kx - 4y = 3; 6x - 12y = 9
Here, a1 = k, b = -4,c1 = 3
a2 = 6, b2 = - 12, c2 = 9
For infinitely many solutions,
Hence, the given system of equation has infinitely many solution if, k = 2.
For x = 3 and y = -1
2x + 3y = 3
⇒ 2 × 3 + 3 × -1 = 3
⇒ 6-3 = 3; which is true.
And 6x + 9y - 9 = 0
⇒ 6 × 3 + 9 × -l -9 = 0
⇒ 18 - 9 - 9 = 0; which is true.
∴ x = 3 and y = -1 is a solution of the given system.
For x = -6 and y = 5
2x + 3y = 3
⇒ 2 × -6 + 3 × 5 = 3
⇒ -12 + 15 = 3; which is true.
⇒ 6x + 9y - 9 = 0
⇒ 6 × -6 + 9 x 5 - 9 = 0
⇒ -36 + 45 - 9 = 0; which is true.
∴ x = -6 and y = 5 is also a solution of the given system.
Yes, the given system of simultaneous linear equations has infinite solutions.
Given the linear equation 2a + 3y - 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is :
(i) parallel lines
(ii) intersecting lines
(iii) coincident lines.
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041907.png)
10x + 5y - (k - 5) = 0
20x + 10y - k = 0.
Here, we have
a1 = 10 b1 = 5 c1 = - (k - 5)
a2 = 20 b2 = 10 c2 = - k
For infinitely many solutions, we have
Hence, the given system of equations has infinitely many solutions, when k = 10.
Solution not provided.
Ans. All real numbers except
Solution not provided.
Ans. All real numbers except-6
Solution not provided.
Ans. No
Solution not provided.
Ans.All real numbers except -4
Solution not provided.
Ans. All real values except ![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041939.png)
.
Solution not provided.
Ans. Infinite solution, equation : 1 and 3; Unique solution, equation : 1 and 2.
Solution not provided.
Ans.Infinite solution, equation : 1 and 3; Unique solution, equation : 1 and 2.
Solution not provided.
Ans. Yes
Solution not provided.
Ans. Yes, consistent
nd 10x + 4y = 50. Also, state, whether system is consistent or inconsistent.
Solution not provided.
Ans. No, inconsistent
Solution not provided.
Ans. x = 2y; 5x + 10y = 60
Solution not provided.
Ans. x - 3y = 0; x - 2y = 12
Solution not provided.
Ans. 80°, 100°, 80° and 100°
Let present age of Manish be x years and present age of Rahim be y years.
Case I. x = 3y
⇒ x - 3y = 0
Case II.
After 5 years :
Age of Manish = (x + 5) years
Age of Rahim = {y + 5) year
Fig. 3.18.
According to question
x + 5 = 2(y + 5)
⇒ x + 5 = 2y + 10
⇒ x - 2y = 10 - 5
⇒ x - 2y = 5
So, algebraic representation be
x - 3y = 0 ...(i)
x - 2y = 5 ...(ii)
Graphical representation
For eqn. (i), we have
x - 3y = 0
⇒ x = 3y
Thus, we have following table :
For eqn. (ii), we have
x - 2y = 5
⇒ x = 5 + 2y
Thus, we have following tables :
When we plot the graph of the equation, we find that both the lines intersect at one point.
Hence, given system of equations has a unique solution.
So, we can say that system is consistent.
Represent the following system of linear equations graphically from the graph find the points where the lines intersect y-axis.
3x + y - 5 = 0, 2x - y - 5 = 0
We have,
3x + y - 5 = 0
⇒ y = 5 - 3x
Thus we have following table :
We have, 2x - y - 5 = 0
⇒ y = 2x - 5
Thus, we have following table :
Fig. 3.19.
When we plot the graph of the given equation, we find that both the lines intersect at the point (-1, 2), therefore x = -1, y = 2 is the solution of the given system of equations.
From the graph we observe that lines intersect y-axis at (-5, 0) and (5,0)
We have x = y
Thus, we have following table :
We have, y = 2x
Thus, we have following table :
We have x + y = 6
⇒ x = 6 - y
Fig. 3.20.
Thus, we have following table :
Co-ordinates of the vertices are (0, 0), (2, 4), (3, 3).
Draw the graphs of the equations :
x - y = 1
and 2x + y = 8
Determine the vertices of the triangle formed by these lines and x-axis.
We have :
x - y = 1
⇒ x = y + 1
Thus, we have following table :
Thus, we have following table :
Fig. 3.21.
When we plot the graph of the given equations, we find that both the lines intersect at the point (3, 2), therefore x = 3, y = 2 is the solution of the given system of equations.
Vertices of triangle are A(3, 2), 13(1, 0), C(4, 0).
We have
x + y = 5
⇒ x = 5 - y
Thus, we have the following table :
We have 3x - y = 3
⇒ y = 3x - 3
Thus, we have following table :
Fig. 3.22.
When we plot the graph of the given equations, we find that both the lines intersect at the point (2, 3), therefore, x = 3, y = 2 is the solution of the given system of equation.
Let the number of shirts be x and the number of jackets be y. Then equations formed are
y = 4x - 3 ...(i)
y = 5x - 4 ...(ii)
We have y = 4x - 3
Thus, we have following table :
We have y = 5x - 4
Thus, we have following table :
Fig. 3.23.
When we plot the graph of both the equations, we find that the two lines intersect at the point (1, 1). So,x = 1,y - 1 is the required solution of the pair of linear equation i.e., the number of jackets he purchased is 1 and the number ofshirts he purchased is 1.
We have, 2x + y = 6
Thus, we have following table ;
Fig. 3.24.
II. We have,
x - 2y = -2
⇒ x = 2y - 2
Thus, we have following table :
When we plot the graph of the given equation, we find that both the lines intersect at the point (2, 2).
From the graph it is clear than the co-ordinates of the points where the lines meet the x-axis are (-2, 0), (3, 0).
Tips: -
Represent the following pair of equations graphically and write the coordinates of points where the lines intersect y-axis :
x + 3y = 6
2x - 3y = 12
The given equations are :
x + 3y = 6 ...(i)
and 2x - 3 y = 12 ...(ii)
From equation (i), we get
x - 6 - 3y
Thus, we have following table
From equation (ii), we get
2x = 3y + 12
Thus, we have following table
When we plot the graph of the given equation, we Find that both the lines intersect at the point (6, 0). So, a = 6, y = 0 is the solution of the given equation. From the graph it is clear that the vertices of triangle. So formed by lines representing given equations and y-axis are (6, 0).
Problems Based on Substitution Method
The given equation are 
Thus, we have,
9x - 10y = -12 ...(i)
2x + 3y = 13 ...(ii)
From (ii), we get
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041996-3.png)
Let the constant expenditure be Rs. x
and consumption of wheat = y quintals
When rate per quintal = Rs. 250 Then,
Total expenditure = constant expenditure +
(consumption × rate per quintal)
Case I.
1000 = x + (y × 250)
⇒ 1000 = x + 250y
Case II. 980 = x + (y × 240)
⇒ 980 = x + 240y
Thus, we have following equations
x + 250y = 1000 ...(i)
x + 240y = 980 ...(ii)
From (i), we have
x = 1000 - 250y ...(iii)
Substituting this value in (ii), we get
(1000 - 250y) + 240y = 980
⇒ 1000 - 250y + 240y = 980
⇒ 1000 - 10y = 980
-10y = 980 - 1000
⇒ -10y = -20
⇒ y = 2
Substituting this value in (iii), we get
x = 1000 - 250 × 2
⇒ x = 1000 - 500
⇒ x = 500
Hence, total monthly expenses = Rs. 500
Now, total expenses when the price of wheat is Rs. 350 per quintal
= x + 350y
= 500 + 350 × 2
= 500 + 700
= Rs. 1200. Ans.
Let the digit at 10’s place by x.
And, digit of unit’s place be y.
Then, Number = 10x + y
Case I. 10x + y = 8(x + y) + 1
⇒10x + y = 8x + 8y + 1
⇒ 10x - 8x + y - 8y = 1
⇒ 2x - 7y = 1
Case II. 10x + y = 13(x - y) + z
⇒ 10x + y = 13x - 13y + 2
⇒ 10x - 13x + y + 13y = 2
⇒ -3x + 14y = 2
Thus, we have, 2x - 7y = 1 ...(i)
-3x + 14y = 2 ...(ii)
From (i), we have 2x - 7y = 1
Subtituting the value of (ii) and (iii), we get
Putting the value of y (iii), we get
Hence, Number = 10x + y
= 10(4) + 1 =4 0 + 1 = 41
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10042021-1.png)
Thus, we have the following systems of linear equations
x - y = 2 ...(i)
4x - y = 80 ...(ii)
and x - y = -2 ...(iii)
Case I : From (i), we have
[Considering (i) and (ii)]
x - y = 2
⇒ x = 2 + y ...(iv)
Substituting the value of x in (ii), we get
4x - y - 80
⇒ 4(2 + y) - y = 80
⇒ 8 + 4y - y = 80
⇒ 8 + 3y = 80 ⇒ 3y = 72
⇒ y = 24
Substituting the value ofy in (iv), we get
x = 2 + y = 2 + 24= 26
Hence, Age of A = 26 years
and Age of B = 24 years
Case II : From (iii), we have
[Considering (ii) and (iii)]
x - y = -2 ⇒ x = y - 2 ...(v)
Putting the value of (v) in (ii), we get
4x - y = 80
Substituting the value ofy in (v), we get
Let the cost price of one chair be Rs. x and that of one table be Rs. y. Profit on chair = 25%.
∴ Selling price of one chair 
Profit on a table = 10%
∴ Selling price of one table = 
According to the given condition, we have
If profit on a chair is 10% and on a table is 25%, then total selling price is Rs. 1535.
Subtracting equation (ii) from equation (i), we get
3x - 3y = -300 ⇒ x - y = -100
Adding equation (ii) and (i), we get
47x + 47y = 61100 ⇒ x + y = 1300
Thus, we have following equations
x - y = -100 ...(iii)
x + y = 1300 ...(iv)
From (iii), we have
x - y = - i 00
⇒ x = y - 100 ...(v)
Substituting the value of x in (iv), we get
x + y = 1300
⇒ y - 100 + y - 1300
2y - 100 = 1300
⇒ 2y - 1400 ⇒ y = 700
Substituting the value of y in (v), we get
x = y - 100
⇒ x = 700 - 100 = 600
Hence, cost price of one chair = Rs. 600 and cost price of one table = Rs. 700
Fig. 3.26.
Let the speeds of two cars be x km./hr. and y km/hr.
Then, according to the given problem,
5x - 5y = 100
⇒ x - y = 20 ...(i)
and x + y = 100 ...(ii)
By adding, we get 2x = 120
⇒ x = 60
By subtracting, we get 2y = 80
⇒ y = 40
Hence, the required speeds of the two cars are: 60 km/hr. and 40 km/hr.
Let the income of first person be Rs. 9x and the income of second person be Rs. 7x. Again, let the expenditures of first and second person be 4y and 3y respectively. Then,
Saving of first person = 9x - 4y
Saving of second person = 7x - 3y
∴ 9x - 4y = 200 ...(i)
and 7x - 3y = 200 ...(ii)
From (i), we have
9x - 4y = 200
Substituting the value of x in (ii), we have![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10042026-1.png)
Substituting the value of y in (iii), we get
Hence, monthly income of First person
= Rs. 9x = Rs. (9 × 200) = Rs. 1800
and monthly income of second person
= Rs. 7x = Rs. (7 × 200) = Rs. 1400.
Problems Based on Elimination Method
Let the speed of the train be x km/hr and that of the car be y km/hr.
We have following cases :
Case I. When he travels 250 km by train and the rest by car:
In this case, we have
Time taken by the man to travel 250 km by train
Time taken by the man to travel (370 - 250)
According to the given condition
Case II. When he travels 130 km by train and the rest by car:
Time taken by the man to travel 130 km by train![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10042027-3.png)
Time taken by the man to travel (370 - 130)
According to the given condition
Thus, we have following system of equations :![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10042027-6.png)
125u + 60 v = 2 ....(i)
130u + 240v = 
Multiplying equation (iii) by 4 the above system of equations becomes
500u + 240v = 8 ...(iii)
130u + 240v = 
Subtracting equation (vi) from equation (iv), we get
5 + 240v = 8
Hence, Speed of the train = 100 km/hr
Speed of the car = 80 km/hr.
Let the digit at 10’s place be x
and digit at unit’s place be y.
∴ Number = 10x + y
Number obtained after reversing the order of the digits = 10y + x
Case I.
10x + y + 10y + x = 66
⇒ 11x + 11y = 66
⇒ 11(x + y) = 66
⇒ x + y = 6 ...(i)
Case II. x - y = ±2
⇒ x - y = + 2 ...(ii)
and x - y = - 2 ...(iii)
Considering (i) and (ii), we get
Putting the value of ‘y’ in (i), we get
x + 2 = 6
⇒ x = 4
So, Number = 10x + y
= 42
Considering (i) and (iii), we get![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10042028-1.png)
Putting the value of ‘y’ in (i), we get
x + y = 6
⇒ x + 4 = 6
⇒ x = 2
So, Number = 10x + y = 24
Thus, there are two such numbers 42 and 24.
Solve the following system of equations by elimination method
6(ax + by) = 3a + 2b
6(bx - ay) =3b - 2a.
We have
6 ax + 6by = 3a + 2b ...(i)
6bx - 6ay = 3b - 2a ...(ii)
For making the coefficient of ‘x’ in (i) and (ii) equal, we multiply eq. (i) by ‘b’ and (ii) by ‘a’ and then subtracting, we get
Let the number of 20 paise coins = x
and number of 25 paise coins = y
Then, value of 20 paise coins = 20x
and value of 25 paise coins = 25y
Case I. x + y = 50
Case II. 20x + 25y = 1125
[∵ 11.25 = 1125 Paise]
Thus, we have
x + y = 50 ...(i)
20x + 25y = 1125 ...(ii)
For making the coefficient of ‘x’ in (i) and (ii) equal, we multiply the (i) by 20 and then subtracting, we get
Putting the value of ‘y’ in (i), we get
x + y = 50
⇒ x + 25 = 50
⇒ x = 25
Hence, the number of 20 paise coins = 25 and the number of 25 paise coins = 25.
Let the initial salary be ‘x’ and increment per year be ‘y’
Case I. Initial salary = x
Increment after 4 years = 4y
According to question
x + 4y = 4500
Case II. Initial salary = x
Increment after 10 years = 10y
According to question
x + 10y = 5400
Thus, we have x + 4y = 4500 ...(i)
x + 10y = 5400 ...(ii)
Since the coefficient of ‘x’ in (i) and (ii) are equal.
So we can simply eliminate the variable ‘x’ by subtracting.
Putting this value in (i), we get
x + 4y = 4500
⇒ x + 4(150) = 4500
⇒ x + 600 = 4500
⇒ x = 3900
Hence, initial salary = Rs. 3900 and annual Increment = Rs. 150.
Problems Based on Cross-Multiplication Method
A motor boat whose speed is 24 km/h in still water takes 1 hour more to go 32km upstream than to return downstream to the same spot. Find the speed of the stream.
Let the speed of the stream be s km/h.
Speed of the motor boat 24 km / h
Speed of the motor -boat upstream 24 s
Speed of the motor boat downstream 24 s
According to the given condition,
Since, speed of the stream cannot be negative, the speed of the stream is 8 km/h.
Let the average speed of train for the first 54 km be x km/h
⇒ Average speed for the next 63 km = ( x + 6) km/h
We know
⇒ 117x + 324 = 3 ( x2 + 6x)
⇒ 117x + 324 = 3x2 + 18x
⇒ 3x2 - 99x -324 = 0 ..(i)
Taking common from the above equation (i)
we have
x2 - 33x - 108 = 0
⇒ x2 - 36x + 3x -108 = 0
⇒ x (x - 36) + 3 (x - 36) = 0
⇒ (x - 36) (x +3 )=0
⇒ x -36 = 0 Or x + 3 =0
x = 36 or x = -3
The speed of the train cannot be negative. Thus, x = 36
Hence, the speed of the train to cover 54 km or its first speed is 36 km/h.
If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear, then find the value of k.
Given points are A( k+1, 2k), B(3k, 2k+3), and C(5k-1, 5k)
These points will be collinear, if area of the triangle formed by them is zero.
We have,
i.e.
Sponsor Area
Sponsor Area
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041548-1.png)
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041661.png)
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041666.png)
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041669.png)
Find the fraction.
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10041675.png)