Pipes And Cistern
Sponsor Area
A cistern has 3 pipes A, B and C. A and B can fill it in 3 and 4 hours respectively, and C can empty it in 1 hour. If the pipes are opened at 3 p.m., 4 p.m. and 5 p.m. respectively on the same day, the cistern will be empty at
-
7 : 12 p.m.
-
7 : 15 p.m.
-
7 : 10 p.m.
-
7 : 18 p.m.
A.
7 : 12 p.m.
Part of the cistern filled by A in 2 hours i.e. till 5 p.m.
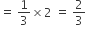
Part of the cistern filled by B in 1 hour i.e. till 5 p.m.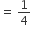
When all three pipes are opened, net part filled in one hour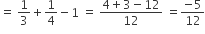
i.e. 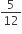 part is emptied per hour.
part is emptied per hour.
∴ Time taken to empty 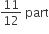
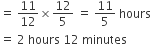
∴ Required time = 5 + 2 : 12 = 7 : 12 p.m.
Sponsor Area
A electric pump can fill a tank in 2 hours. Because of a leak in the tank, it was taking  to fill the tank. The leak can drain all the water off the tank in how many hours?
to fill the tank. The leak can drain all the water off the tank in how many hours?
-
9 hours
-
10 hours
-

-

B.
10 hours
Let the leak can drain all the water off the tank = x hours
According to the question,
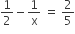

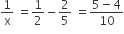

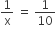
 x = 10 hours
x = 10 hours
A swimming pool has 3 drain pipes. The first two pipes A and B, operating simultaneously can empty the pool in half the time that C, the 3rd pipe alone takes to empty it. Pipe A, working alone, takes to empty it. Pipe A, working alone, takes half the time taken by pipe B. Together they take 6 hours 40 minutes to empty the pool. Time taken by pipe A to empty the pool, in hours, is
-
15
-
10
-
30
-
17
A.
15
Let the time taken by pipe B to empty the tank = 2x hours
∴ Time taken by pipe A to empty the tank = x hours
(A and B) takes half of the time that c takes.
∴ Time taken by pipe C
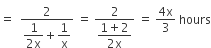
A, B and C together take 6 hours 40 minutes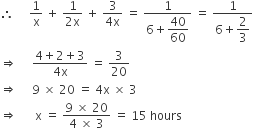
A tank can be filled by pipe A in 2 hours and pipe B in 6 hours. At 10 A.M. pipe A was opened. At what time will the tank be filled if pipe B is opened at 11 A.M.?
-
12.45 A.M.
-
5 P.M.
-
11.45 A.M.
-
12 P.M.
C.
11.45 A.M.
Part filled by A in 1 hour (i.e. till 11 A.M.) = 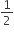
Part filled by A and B in 1 hour (60 minutes):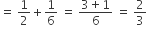
Time taken by A and B to fill 
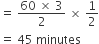
∴ Tank will be filled at 11.45 A.M.
A tank has two pipes. The first and pipe can fill it in 4 hours and the second can empty it in 16 hours. If two pipes be opened together at a time, then the tank will be filled in
-

-
10 hours
-
6 hours
-

D.

Part of tank filled by both the pipes in 1 hour
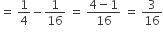
∴ Required time = 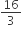

Sponsor Area
Mock Test Series
Mock Test Series





