Average
Sponsor Area
5 members of a team are weighted consecutively and their average weight calculated after each member is weighed. If the average weight increases by one kg each time, how much heavier is the last player than the first one?
-
4 kg
-
20 kg
-
8 kg
-
5 kg
C.
8 kg
Shortcut Method:We have to find out the weight of a person let's suppose 16th, just add a number prior to that i.e. 15 so, weight would be (16 + 15) = 31 kg
Thus,
Weight of first person = 1 + 0 = 1 kg
Weight of fifth person = 5 + 4 = 9 kg
Hence, difference of their weights = 9 - 1 = 8 kg.
Sponsor Area
A and B have their annual average income Rs. 80,000. B and C have their annual average income Rs. 75,000. C and A have their annual average income Rs. 78,000.The annual income of A is?
-
Rs. 81000
-
Rs. 82000
-
Rs. 83000
-
Rs. 84000
C.
Rs. 83000
Average annual income of A and B = 80000
Total annual income of A and B = 80000 x 2 = Rs. 160000 ...(i)
Similarly,
Total annual income of B and C = 75000 x 2 = Rs. 150000...(ii)
Total annual income of C and A = 78000 x 2 = Rs. 156000...(iii)
On Adding all three,
Total annual income of 2(A + B + C) = Rs. (160000+150000+156000)
= Rs. 466000
Total annual income of (A + B + C) = Rs .233000 ...(iv)
A's annual income = Equation (iv) - (ii)
= Rs. (233000 - 150000)
= Rs. 83000
A batsman in his 12th innings makes a score of 63 runs and thereby increases his average score by 2. The average of his score after 12th innings is
-
41
-
42
-
34
-
35
A.
41
Let he scores x runs before 12th innings.
Therefore,
⟹ 12 (x + 2) - 11x = 63
⟹ 12x + 24 - 11x = 63
⟹ x + 24 = 63
⟹ x = 39
Hence, his score after 12th innings shall be (39 + 2) = 41 runs.
A cricket player has an average score of 30 runs of 42 innings played by him. In an innings, his highest score exceeds his lowest score by 100 runs. If these two innings are excluded, his average of the remaining 40 innings is 28 runs. His highest score in an innings is
-
125
-
120
-
110
-
100
B.
120
Let the lowest score of the cricketer be x.
∴ Cricketer's highest score would be (x + 100)
According to the question,
x + (x + 100) = 42 x 30 - 40 x 28
⟹ 2x + 100 = 1260 - 1120 = 140
⟹ 2x = 40
⟹ x = 20
∴ His highest score in an innings = (x + 100) = (20 + 100) = 120.
A student, by mistake, wrote 64 in place of 46 as a number at the time of finding the average of 10 given and got the average as 50. The correct average of the number is:
-
48.2
-
48
-
48.1
-
49
A.
48.2
Required Average:
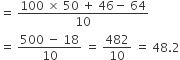
Sponsor Area
Mock Test Series
Mock Test Series





