If  then find the value of n.
then find the value of n.
-
2
-
3
-
4
-
5
D.
5
We have, 
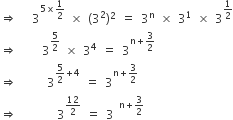
If base will be same, then comparing the exponent,
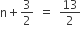
Sponsor Area
If  then find the value of n.
then find the value of n.
2
3
4
5
D.
5
We have, 
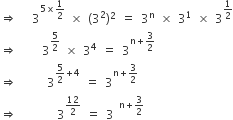
If base will be same, then comparing the exponent,
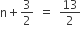
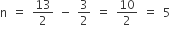
Sponsor Area
The value of 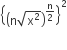 is
is
x


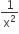
C.

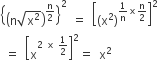
The value of 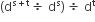 would be
would be
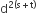
1
0

B.
1
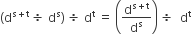
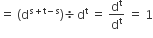
When xm is multiplied by xn ,product is 1. The relation between m and n is
mn = 1
m = n
m + n = 1
m = - n
D.
m = - n

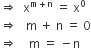
If 2x+4 - 2x+2 = 3, then the value of 'x' is
0
2
-1
-2
D.
-2
Shortcut Method:
Start putting the value of option which equates the equation.
e.g. put x = -2
2x+4 - 2x+2 = 3
2-2+4 - 2-2+2 = 3
22 - 20 = 3
4 - 1 = 3
Sponsor Area
Mock Test Series