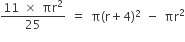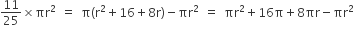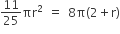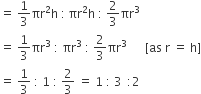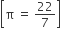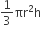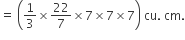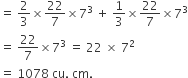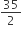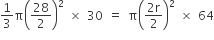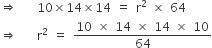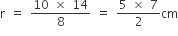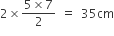A ball of lead 4 cm in diameter is covered with gold. If the volume of the gold and lead are equal, then the thickness of gold [given 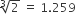 ] is approximately.
] is approximately.
-
5.038 m
-
5.190 cm
-
1.038 cm
-
0.518 cm
D.
0.518 cm
Diameter of lead = 4 cm
Radius of lead = 2 cm
Volume of lead = 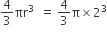
Let the thickness of gold be x cm, then
Volume of gold = 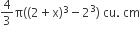
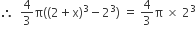
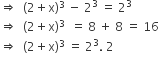
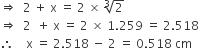






 that of the pool, then the radius (in m) of the pool is
that of the pool, then the radius (in m) of the pool is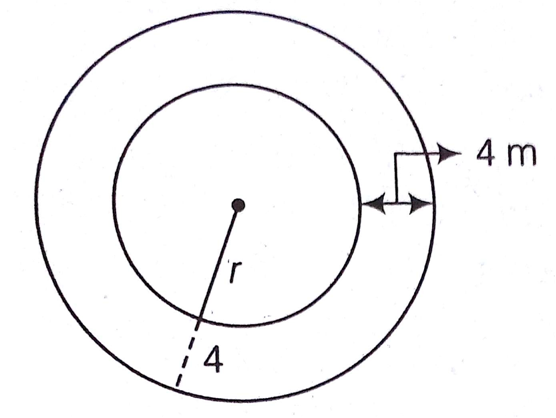
 Area of wall =
Area of wall = 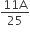
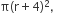 Area of pool =
Area of pool =