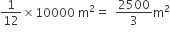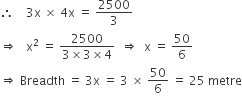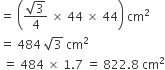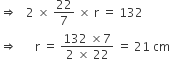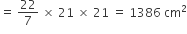Perimeter of a rhombus is 2p unit and sum of length of diagonals is m unit, then area of the rhombus is

• 
• 
• 
• 

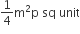
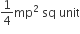
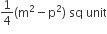
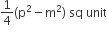
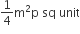
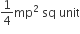
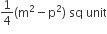
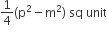
C.

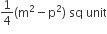
Let d₁, d₂ be the diagonals of the rhombus
Perimeter of rhombus (P) =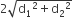 
                         Perimeter = 2p(given)
∴       
Squaring both the sides, we get
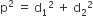                ...(i)
Now, sum of diagonals (d₁ + d₂) =  m (given)
  Again, Squaring both the sides, we get
               
         
         
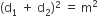
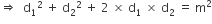
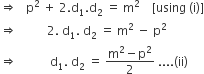
Area of rhombus =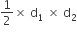 
                        
                          
 
         

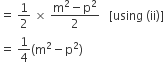
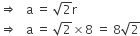
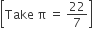
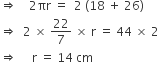
The area of the square inscribed in a circle of radius 8 cm is

• 256 sq. cm.

• 250 sq. cm.

• 128 sq. cm.

• 125 sq. cm.

A circle and a rectangle have the same perimeter. The sides of the rectangle are 18 cm and 26 cm. The area of the circle is 

• 125 cm²

• 230 cm²

• 550 cm²

• 616 cm²

A lawn is in the form of a rectangle having its breadth and length in the ratio 3 : 4. The area of the lawn is . The breadth of the lawn is

• 25 metres

• 50 metres

• 75 metres

• 100 metres

A piece of wire 132 cm long is bent successively in the shape of an equilateral triangle, a square and a circle. Then area will be longest in shape of

• Circle

• Equilateral triangle

• Square

• Equal in all the shapes