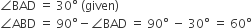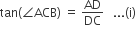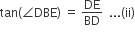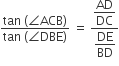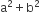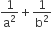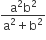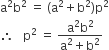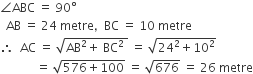+91-8076753736 [email protected]

Geometry - Triangles

Sponsor Area

Question

Wired Faculty App

$angle straight A comma space angle straight B comma space angle straight C$ are three angles of a triangle, If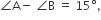 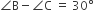$angle straight A minus space angle straight B space equals space 15 degree comma$ $angle straight B minus angle straight C space equals space 30 degree$ , then $angle straight A comma space angle straight B space and space angle straight C$ are

80°, 60°, 40°

70°, 50°, 60°

80°, 65°, 35°

80°, 55°, 45°

Solution

C.

80°, 65°, 35°

∠A + ∠B + ∠C = 180° ...(i)
(∠B - ∠C) - (∠A - ∠B ) = 30° - 15°
⟹ 2∠B - ∠A - ∠C = 15° ...(ii)
By adding (i) and (ii),
3∠B = 180° + 15° = 195°
⟹ ∠B = 65°
∠A - ∠B = 15°
⟹ ∠A = 15° + 65° = 80°
∠C = ∠B - 30°
= 65° - 30° = 35°

Sponsor Area

Question

Wired Faculty App

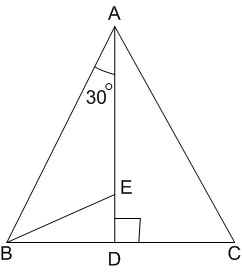
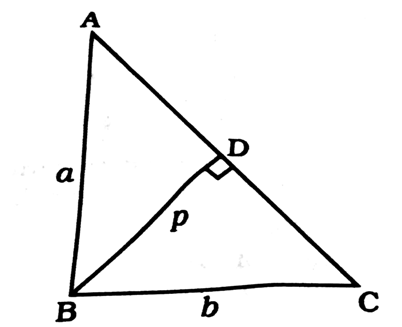
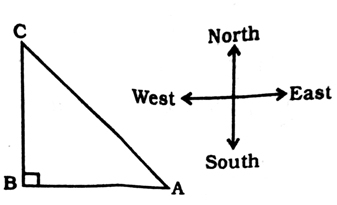
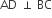D is a point on the side BC of a triangle ABC such that $AD space perpendicular space BC$ . E is a point on AD for which AE : ED = 5 : 1. If $angle BAD space equals space 30 degree$ and then 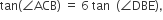$tan left parenthesis angle ACB right parenthesis space equals space 6 space tan space space left parenthesis angle DBE right parenthesis comma$ then $angle ACB space equals$

30°

45°

60°

15°

Solution

C.

60°

angle BAD space equals space 30 degree space left parenthesis given right parenthesis angle ABD space equals space 90 degree minus angle BAD space equals space 90 degree space minus space 30 degree space equals space 60 degree

Now,

tan left parenthesis angle ACB right parenthesis space equals space AD over DC space space space... left parenthesis straight i right parenthesis

tan left parenthesis angle DBE right parenthesis space equals space DE over BD space space... left parenthesis ii right parenthesis

Divide (i) by (ii)

fraction numerator tan space left parenthesis angle ACB right parenthesis over denominator tan space left parenthesis angle DBE right parenthesis end fraction space equals space fraction numerator begin display style AD over DC end style over denominator begin display style DE over BD end style end fraction

rightwards double arrow space space 6 over 1 space cross times space 1 space space equals space AD over DC space cross times space BD over DE rightwards double arrow space space 6 space cross times space BD over DC space equals space 6 rightwards double arrow space space space BD space equals space DC space space space space space left square bracket AD space is space bisecting space the space BC space in space the space ratio space 1 space colon space 1 right square bracket therefore space space space angle ACB space equals space 60 degree

Thus, ΔABC is an equilateral triangle.

Question

Wired Faculty App

a and b are two sides of adjacent to the right angle of a right-angled and p is the perpendicular drawn to the hypotenuse from the opposite vertex. Then p² is equal to

$straight a squared plus straight b squared$
$1 over straight a squared plus 1 over straight b squared$
$fraction numerator straight a squared straight b squared over denominator straight a squared plus straight b squared end fraction$
$straight a squared minus straight b squared$

Solution

C.

fraction numerator straight a squared straight b squared over denominator straight a squared plus straight b squared end fraction

BD perpendicular AC AB perpendicular space BC

Now, Hypotenuse (H) of ΔABC

equals space square root of AB squared space plus space BC squared end root equals space square root of straight a squared plus straight b squared end root

Area of ΔABC =

1 half cross times AB space cross times space AC space equals space 1 half cross times AC cross times BD

rightwards double arrow space AB space cross times space BC space equals space AC space cross times space BD rightwards double arrow space space space space ab space equals space square root of straight a squared plus straight b squared end root space cross times space straight p

On squaring both sides,

straight a squared straight b squared space equals space left parenthesis straight a squared plus straight b squared right parenthesis straight p squared therefore space space space straight p squared space equals space fraction numerator straight a squared straight b squared over denominator straight a squared plus straight b squared end fraction

Question

Wired Faculty App

A man goes 24 m due west and then 10 m due north. Then the distance of him from the starting point is

17 m

26 m

28 m

34 m

Solution

B.

26 m

angle ABC space equals space 90 degree space space AB space equals space 24 space metre comma space space BC space equals space 10 space metre therefore space space AC space equals space square root of AB squared plus space BC squared space end root space equals space square root of 24 squared plus 10 squared end root space space space space space space space space space space space space equals space square root of 576 plus 100 end root space equals space square root of 676 space equals space 26 space metre

Question

Wired Faculty App

A point D is taken from the side BC of a right-angled triangle ABC, where AB is hypotenuse. Then

AB² + CD² = BC² + AD²

CD² + BD² = 2 AD²

AB² + AC² = 2AD²

AB² = AD² + BD²

Solution

A.

AB² + CD² = BC² + AD²

AB² = AC² + BC²
AD² = AC² + CD²
⟹ AD² - CD² = AC²
∴ AB² + AC² = AC² + BC² + AD² - CD²
⟹ AB² = BC² + AD² - CD²
⟹ AB² + CD² = BC² + AD²

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

6