+91-8076753736 [email protected]

Geometry - Quadrilaterals and Polygons

Sponsor Area

Question

Wired Faculty App

ABCD is a cyclic quadrilateral and AD is a diameter. If ∠DAC = 55° then value of ∠ABC is

55°

35°

145°

125°

Solution

C.

145°

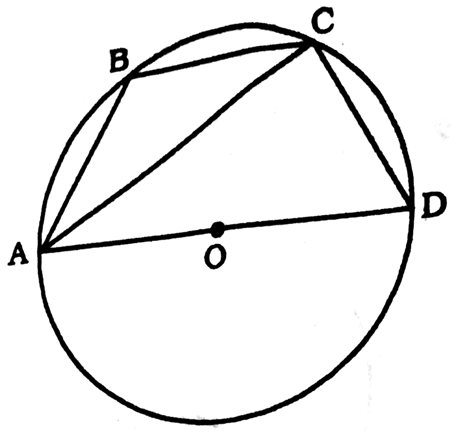
In ΔACD
∠DAC = 55°
∠ACD = 90°
∠D = 180° - 55° - 90° = 35°
∴ ∠ABC + ∠ADC = 180°
⟹ ∠ABC = 180° - 35° = 145°

Sponsor Area

Question

Wired Faculty App

ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If $angle APB space equals space 110 degree$ and $angle CBD space equals space 30 degree$ , then $angle ADB$ measures

$80 degree$
$70 degree$
$30 degree$
$55 degree$

Solution

A.

80 degree

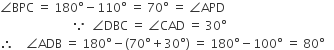
angle BPC space equals space 180 degree minus 110 degree space equals space 70 degree space equals space angle APD space space space space space space space space space space space space space space space space space space space space space space space space space because space space angle DBC space equals space angle CAD space equals space 30 degree therefore space space space space angle ADB space equals space 180 degree minus left parenthesis 70 degree plus 30 degree right parenthesis space equals space 180 degree minus 100 degree space equals space 80 degree space space space

Question

Wired Faculty App

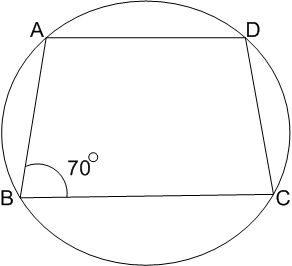
ABCD is a cyclic trapezium in which AD || BC. If $angle ABC space equals space 70 degree$ , then $angle BCD$ is

110°

80°

70°

90°

Solution

C.

70°

ABCD is a cyclic trapezium in which AD || BC. If , then &nbs

angle ABC space equals space 70 degree space left parenthesis given right parenthesis angle ADC space equals space 180 degree space minus space 70 degree space equals space 110 degree space space left square bracket Sum space of space opposite space angles space of space cyclic space quadrilateral right square bracket

angle BCD space equals space 180 degree minus 110 degree space equals space 70 degree space space left square bracket Adjacent space angles space of space straight a space parallelogram right square bracket

Question

Wired Faculty App

ABCD is a rectangle where the ratio of the lengths of AB and BC is 3 : 2. If P is the mid point of AB, then the value of 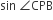$sin space angle CPB$ is

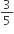
$3 over 5$
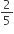
$2 over 5$
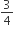
$3 over 4$
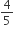
$4 over 5$

Solution

D.

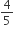
4 over 5

AB = 3x units (given)
BC = 2x units (given)

As P is the mid point of AB
∴

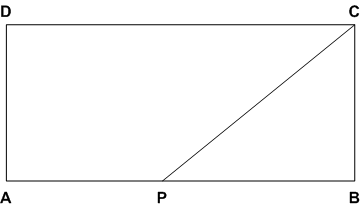
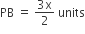
PB space equals space fraction numerator 3 straight x over denominator 2 end fraction space units

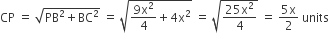
CP space equals space square root of PB squared plus BC squared end root space equals space square root of fraction numerator 9 straight x squared over denominator 4 end fraction plus 4 straight x squared end root space equals space square root of fraction numerator 25 straight x squared over denominator 4 end fraction end root space equals space fraction numerator 5 straight x over denominator 2 end fraction space units

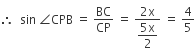
therefore space space sin space angle CPB space equals space BC over CP space equals space fraction numerator 2 straight x over denominator begin display style fraction numerator 5 straight x over denominator 2 end fraction end style end fraction space equals space 4 over 5

Question

Wired Faculty App

ABCD is a trapezium with AD and BC parallel sides. E is a point on BC. The ratio of the area of ABCD to that of AED is

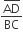
$fraction numerator AD with bar on top over denominator BC end fraction$
$fraction numerator BE with bar on top over denominator EC with bar on top end fraction$
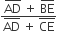
$fraction numerator AD with bar on top space plus space BE with bar on top over denominator AD with bar on top space plus space CE with bar on top end fraction$
$fraction numerator AD with bar on top space plus space BC with bar on top over denominator AD with bar on top end fraction$

Solution

D.

fraction numerator AD with bar on top space plus space BC with bar on top over denominator AD with bar on top end fraction

EF is perpendicular on side AD.
∴ Area of trapezium

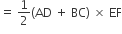
equals space 1 half left parenthesis AD space plus space BC right parenthesis space cross times space EF

Area of ΔAED =

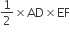
1 half cross times AD cross times EF

∴ Required ratio

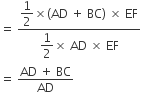
equals space fraction numerator begin display style 1 half end style cross times left parenthesis AD space plus space BC right parenthesis space cross times space EF over denominator begin display style 1 half end style cross times space AD space cross times space EF end fraction equals space fraction numerator AD space plus space BC over denominator AD end fraction

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

11