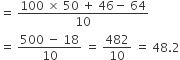+91-8076753736 [email protected]
logo
logo

Average

Sponsor Area

Question
SSCCGLENQA12042965
Wired Faculty App

5 members of a team are weighted consecutively and their average weight calculated after each member is weighed. If the average weight increases by one kg each time, how much heavier is the last player than the first one?

  • 4 kg

  • 20 kg

  • 8 kg

  • 5 kg

Solution

C.

8 kg

Shortcut Method:
We have to find out the weight of a person let's suppose 16th, just add a number prior to that i.e. 15 so, weight would be (16 + 15) = 31 kg
Thus,
Weight of first person  = 1 + 0 = 1 kg
Weight of fifth person  = 5 + 4 = 9 kg
Hence, difference of their weights  = 9 - 1 = 8 kg.

Sponsor Area

Question
SSCCGLENQA12042463
Wired Faculty App

A and B have their annual average income Rs. 80,000. B and C have their annual average income Rs. 75,000. C and A have their annual average income Rs. 78,000.The annual income of A is?

  • Rs. 81000

  • Rs. 82000

  • Rs. 83000

  • Rs. 84000

Solution

C.

Rs. 83000

Average annual income of A and B = 80000
Total annual income of A and B = 80000 x 2 = Rs. 160000 ...(i)
Similarly, 
Total annual income of B and C = 75000 x 2 = Rs. 150000...(ii)
Total annual income of C and A = 78000 x 2 = Rs. 156000...(iii)
On Adding all three,
Total annual income of 2(A + B + C) = Rs. (160000+150000+156000)
                                                     = Rs. 466000
 Total annual income of (A + B + C) = Rs .233000   ...(iv)
A's annual income  = Equation (iv) - (ii)
                           = Rs. (233000 - 150000)
                           = Rs. 83000

Question
SSCCGLENQA12043101
Wired Faculty App

A batsman in his 12th innings makes a score of 63 runs and thereby increases his average score by 2. The average of his score after 12th innings is

  • 41

  • 42

  • 34

  • 35

Solution

A.

41

Let he scores x runs before 12th innings.
Therefore, 
⟹ 12 (x + 2) - 11x = 63
⟹ 12x + 24 - 11x = 63
⟹ x + 24 = 63
⟹ x = 39
Hence, his score after 12th innings shall be (39 + 2) = 41 runs.

Question
SSCCGLENQA12042099
Wired Faculty App

A cricket player has an average score of 30 runs of 42 innings played by him. In an innings, his highest score exceeds his lowest score by 100 runs. If these two innings are excluded, his average of the remaining 40 innings is 28 runs. His highest score in an innings is

  • 125

  • 120

  • 110

  • 100

Solution

B.

120

Let the lowest score of the cricketer be x. 
∴  Cricketer's highest score would be (x + 100)
According to the question,
x + (x + 100) =  42 x 30 - 40 x 28
⟹  2x + 100 = 1260 - 1120 = 140
⟹  2x = 40
⟹   x =  20
∴  His highest score in an innings = (x + 100) = (20 + 100) = 120.

Question
SSCCGLENQA12043491
Wired Faculty App

A student, by mistake, wrote 64 in place of 46 as a number at the time of finding the average of 10 given and got the average as 50. The correct average of the number is:

  • 48.2

  • 48

  • 48.1

  • 49

Solution

A.

48.2

Required Average:

    equals space fraction numerator 100 space cross times space 50 space plus space 46 minus space 64 over denominator 10 end fraction equals space fraction numerator 500 space minus space 18 over denominator 10 end fraction space equals space 482 over 10 space equals space 48.2

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

2