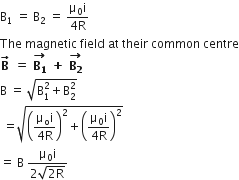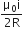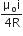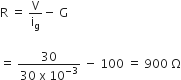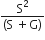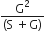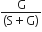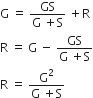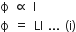Wired Faculty
Sponsor Area
A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. if the current in the loop is i. The resultant magnetic field due to the two semicircular parts at their common centre is
A.
Sponsor Area
A galvanometer has a coil of resistance 100 Ω and gives a full-scale deflection for 30 mA current. If it is to work as a voltmeter of 30 V range, the resistance required to be added will be
900 Ω
1800
500 Ω
1000 Ω
A.
900 Ω
Required resistance 
A galvanometer of resistance 50 Ω is connected to a battery of 3 V along with a resistance of 2950 Ω in series. A full-scale deflection of 30 divisions is obtained in the galvanometer. In order to reduce this deflection to 20 divisions, the resistance in series should be
5050 Ω
5550 Ω
6050 Ω
4450 Ω
D.
4450 Ω
Current through the galvanometer 
A galvanometer of resistance, G is shunted by a resistance S ohm. To keep the main current in the circuit unchanged,the resistance to be put in series with the galvanometer is
C.
Current will be unchanged if resistance remains same so
A long solenoid has 500 turns. When a current of 2 A is passed through it, the resulting magnetic flux linked with each turn of the solenoid is 4 x 10-3 Wb. The self -inductance of the solenoid is
2.5 H
2.0 H
1.0 H
4.0 H
C.
1.0 H
The inductance of a coil is numerically equal to the emf induced in the coil when the current in the coil changes at the rate of 1 As-1. If I is the current flowing in the circuit, then flux linked with the circuit is observed to be proportional to I, ie,
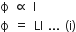
where L is called the self-inductance or coefficients of self-inductance or coefficient of self-inductance or simply inductance of the coil.
Net flux through the solenoid.
Φ = 500 x 4 x 10-3 = 2 Wb
Or 2 = L x 2 [after putting value in eq. or L = 1H]
Sponsor Area
Mock Test Series
