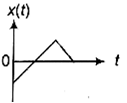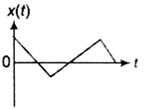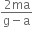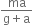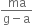Motion In A Plane
Sponsor Area
 are two vectors and θ is the angle between them if
are two vectors and θ is the angle between them if 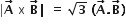 the value of θ is:
the value of θ is:
-
60o
-
45o
-
30o
-
90o
60o
45o
30o
90o
A.
60o
Sponsor Area
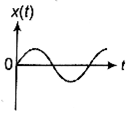
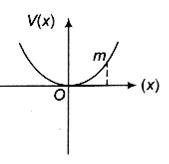
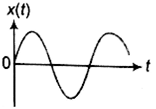
A particle of mass m is released from rest and follows a parabolic path is shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time?
D.
Potential V (x) versus x is parabolic, SHM starts from an extreme position and x versus t should be a cosin curve.
A balloon with mass m is descending down with an acceleration a (where a <g). How much mass should be removed from it so that it starts moving up with an acceleration a?
A.
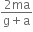
When the balloon is descending down with acceleration a,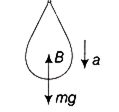
So, mg - B = mx A ... (i)
where B is the buoyant force.
We assume here that while removing same mass, the volume of balloon and hence buoyant force will not change.
Let, us assume the new mass of the balloon is m'.
So, mass removed is (m-m')
Therefore,
B-m'g = m'x a ... (ii)
On solving equations (i) and (ii), we have
mg - B = m x a
B - m'g = m' x a
mg - m'g = ma + m'a
(mg - ma) = m' (g+a) = m (g-a) = m' (g+a)
That is,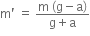
That is, mass removed is m-m'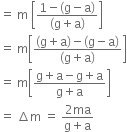
A body is moving with velocity 30 m/s towards east. After 10 s its velocity becomes 40 m/s towards the north. The average acceleration of the body is
-
7 m/s2
-

-
5 m/s2
-
1 m/s2
C.
5 m/s2
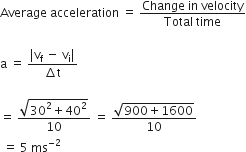
A body of mass 1 kg begins to move under the action of a time dependent force F = 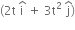 N, where
N, where  are units vectors along X and Y axis. What power will be developed by the force at the time (t)?
are units vectors along X and Y axis. What power will be developed by the force at the time (t)?
-
(2t2 + 4t4) W
-
(2t3 + 3 t4) W
-
(2t3 + 3t5) W
-
(2t + 3t3)W
C.
(2t3 + 3t5) W
A body of mass 1 kg begins to move under the action of time dependent force,
F = (2t  +3t2
+3t2 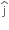 ) N,
) N,
where  are unit vectors along X and Y axis.
are unit vectors along X and Y axis.
F = ma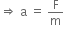
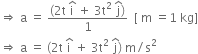
Acceleration, a = 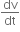

Integrating both sides, we get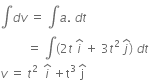
Power developed by the force at the time t will be given as,
P = F.v = (2t  + 3t2
+ 3t2 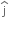 ).(
).(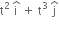 )
)
= (2t. t2 + 3t2.t3)
P = (2t3 + 3t5) W
Sponsor Area
Mock Test Series
Mock Test Series