Mechanical Properties Of Fluids
Sponsor Area
A certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
-
Energy = 4VT
is released. -
Energy = 3VT
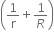is absorbed -
Energy = 3 VT
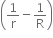is released -
Energy is neither absorbed nor released.
C.
Energy = 3 VT 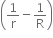is released
If the surface area changes, it will change the surface energy also.
When the surface area decreases, it means energy is released ad vice-versa.
Change in surface energy is 
... (i)
Let, there be n number of drops initially.
So, 
... (ii)
Volume is constant.
So,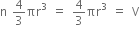 
... (iii)
From equations (ii) and (iii), we have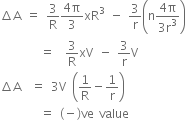
Since, R > r, 
A is negative.
That is, the surface area is decreased.
Hence, energy must be released.
Energy released = 
In the above expression, (-)ve sign shows that amount of energy is released.
Sponsor Area
A U tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of 10 mm above the water level on the other side. Meanwhile, the water rises by 65 mm from its original level (see diagram). The density of the oil is
-
650 kg m–3
-
425 kg m–3
-
800 kg m–3
-
928 kg m–3
D.
928 kg m–3
hoil ρoil g = hwater ρwater g
140 × ρoil= 130 × ρwater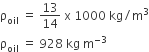
If dimensions of critical velocity vc of a liquid flowing through a tube are expressed as 
are the coefficient of viscosity of liquid, density of liquid and radius of the tube respectively, then the values of x, y and z are given by
-
1,-1,-1
-
-1,-1,1
-
-1,-1,-1
-
1,1,1
A.
1,-1,-1
According to the principle of homogeneity of dimension states that, a physical quantity equation will be dimensionally correct if the dimension of all the terms occurring on both sides of the equations is same.
Given critical velocity of liquid flowing through a tube are expressed as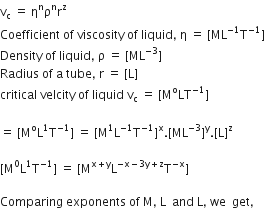
x+ y = 0, - x-3y+z = 1, -x = -1
z = -11 x = 1, y = -1
The wettability of a surface by a liquid depends primarily on
-
viscosity
-
surface tension
-
density
-
angle of contact between the surface and the liquid
D.
angle of contact between the surface and the liquid
The value of angle of contact determines whether a liquid will spread on the surface or not.
The wind with speed 40 m/s blows parallel to the roof of a house. The area of the roof is 250m2. Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be( pair = 1.2 kg/m3)
-
4.8 x 105 N, downwards
-
4.8 x105 N , upwards
-
2.4 x 105 N , upwards
-
2.4 x 105 N , upwards
C.
2.4 x 105 N , upwards
From Bernoulli's theorem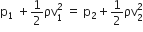
Where p1,p2 are pressure inside and outside the roof and v1, v2 are velocities of the wind inside and outside the roof. Neglect the Width of the roof.
Pressure difference is
p1 -p2 =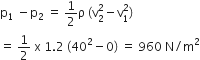
Force acting on the roof is given by
F= (p1 -p2) A = 960 x 250
= 24 x 104 N = 24 x 105 N
As the pressure inside the roof is more than outside to it. So the force will act in the upward direction i.e. F = 24 x 105 N -upward.
Sponsor Area
Mock Test Series
Mock Test Series