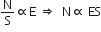A beam of cathode rays is subjected to crossed Electric (E) and magnetic field (B). The fields are adjusted such that the beam is not deflected. The specific charge of the cathode rays is given by
(Where V is the potential difference between cathode and anode)
-
B2/2VE2
-
2VB2/E2
-
2VE2/B2
-
2E2/2VB2
D.
2E2/2VB2
As the electron beam is not deflected,
then
Fm = Fe
Or BeV = Ee
Or v= E/B .... (i)
As the electron moves from the cathode to anode, its potential energy at the cathode appears as its kinetic energy at the anode. If V is the potential difference between the anode and cathode, then potential energy of the electron at cathode = eV. Also, the kinetic energy of the electron at anode = mv2 /2. According to law of conservation of energy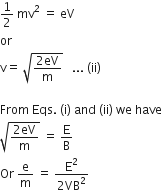









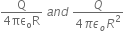

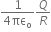

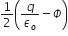
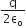
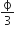

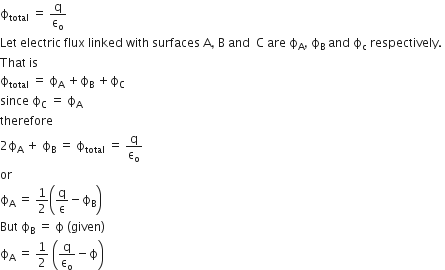
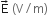 , also in the plane of the paper, is limited only to the lower half of the square surface, (see figure). The electric flux in SI units associated with the surface is
, also in the plane of the paper, is limited only to the lower half of the square surface, (see figure). The electric flux in SI units associated with the surface is
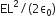


 is a measure of the number of field lines crossing a surface. The number of field lines passing through unit area (N/S) will be proportional to the electric field, or,
is a measure of the number of field lines crossing a surface. The number of field lines passing through unit area (N/S) will be proportional to the electric field, or,