+91-9350504919 support@wiredfaculty.com
Wired Faculty Logo
Wired Faculty Logo Wired Faculty

The Solid State

Sponsor Area

Question
CBSEENCH12011071
Wired Faculty App

A given metal crystallises out with a cubic structure having edge length of 361 pm. If there are four metal atoms in one unit cell, what is the radius of one atom.

  • 40 pm

  • 127 pm

  • 80 pm

  • 108 pm

Solution

B.

127 pm

Given, edge length = 361 pm
Four metal atoms in one unit cell
i.e effective number in unit cell (z) = 4 (given)
therefore,
It is a FCC structure
Face diagonal  = 4r

square root of 2 straight a end root space equals space 4 straight r space equals space straight r equals space fraction numerator square root of 2 space end root space straight x space 361 over denominator 4 end fraction space equals space 127 space pm

Sponsor Area

Question
CBSEENCH12011148
Wired Faculty App

A metal crystallises with a face-centered cubic lattice. The edge of the unit cell is 408 pm. The diameter of the metal atom is

  • 288 pm

  • 408 pm

  • 144 pm

  • 204 pm

Solution

A.

288 pm

For fcc lattice,
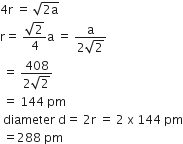
WiredFaculty

Question
CBSEENCH12011120
Wired Faculty App

A metal has a fcc lattice. The edge length of the unit cell is 404 pm. The density of the metal is 2.72 g cm-3. The molar mass of the metal is (NA Avogadro's constant= 6.02 x 1023 mol-1)

  • 40 g mol-1

  • 30 g mol-1

  • 27 g mol-1

  • 20 g mol-1

Solution

C.

27 g mol-1

Given, cell is fcc, So Z =4
Edge length, a = 404 pm = 4.04 x 10-8 cm
Density of metal, d = 2.72 g cm-3
NA = 6.02 x 1023 mol-1
Molar mass ofg the metal, M =?
We know that


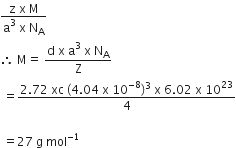
density, d=  WiredFaculty

Question
CBSEENCH12011238
Wired Faculty App

A solid compound XY has NaCl structure. If the radius of the cation is 100 pm, the radius of the anion (Y-) will be 

  • 275.1 pm

  • 322.5 pm

  • 241.5 pm

  • 165.7 pm

Solution

C.

241.5 pm

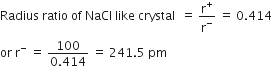
WiredFaculty

Question
CBSEENCH12011171
Wired Faculty App

A structure of a mixed oxide is cubic close packed (ccp). The cubic unit cell of mixed oxide is composed of oxide ions. One fourth of the tetrahedral voids are occupied by divalent metal A and the octahedral voids are occupied by a monovalent metal B. The formula of the oxide is

  • ABO2

  • A2BO2

  • A2B3O4

  • AB2O2

Solution

D.

AB2O2

According to ccp,
Number of O2- ions = 4
So, tetrahedral void = 8
and octahedral void = 4
Since A ions occupied 1/4th of the tetrahedral void.
Therefore,
Number of A ions = 1/4 x 8 = 2
Again, B ions occupied all octahedral void.
Therefore, Number of B ions = 4 
A: B:O = 2:4:4
 = 1:2:2
Structure of oxide= AB2O2

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

1