+91-8076753736 support@wiredfaculty.com
Wired Faculty Logo
Wired Faculty Logo Wired Faculty

Dual Nature of Radiation and Matter

Sponsor Area

Question
CBSEENPH12040079
Wired Faculty App

A  5 W source emits monochromatic light of wavelength 5000 A. When placed 0.5 m away, it liberates photoelectrons from a photosensitive metallic surface. when the source si moved to a distance of 1.0 m, the number of photoelectrons liberated will be reduced by a factor  of:

  • 4

  • 8

  • 16

  • 2

Solution

A.

4

The intensity of light is inversely proportional to the square of the distance.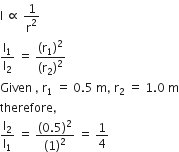
straight I space proportional to space 1 over straight r squared straight I subscript 1 over straight I subscript 2 space equals space fraction numerator left parenthesis straight r subscript 1 right parenthesis squared over denominator left parenthesis straight r subscript 2 right parenthesis squared end fraction Given space comma space straight r subscript 1 space equals space 0.5 space straight m comma space straight r subscript 2 space equals space 1.0 space straight m therefore comma straight I subscript 2 over straight I subscript 1 space equals space fraction numerator left parenthesis 0.5 right parenthesis squared over denominator left parenthesis 1 right parenthesis squared end fraction space equals space 1 fourth
Now, since number of photoelectric emitted per second is directly proportional intensity, so number of electrons emitted would decrease by factor of 4.

Sponsor Area

Question
CBSEENPH12039790
Wired Faculty App

A black body is at a temperature of 5760 K. The energy of radiation emitted by the body at wavelength 250 nm is U1, at wavelength 500 nm is U2 and that at 1000 nm is U3. Wien's constant, b = 2.88 x 106 nmK. Which of the following is correct?

  • U3 = 0

  • U1 > U2

  • U2 > U1

  • U1 = 0

Solution

C.

U2 > U1

Given, temperature, T1 = 5760 K
Given that energy of radiation emitted by the body at wavelength 250 nm in U1, at wavelength 500 nm is U2 and that at 1000 nm is U3.
Now, according to Wein's law, we get
straight lambda subscript straight m straight T space equals space straight b
where, b = Wien's constant = 2.88 x 106 nmK
rightwards double arrow space straight lambda subscript straight m space equals space straight b over straight T
rightwards double arrowstraight lambda subscript straight m space equals space fraction numerator 2.88 space straight x space 10 to the power of 6 space nmk over denominator 5760 space straight K end fraction
rightwards double arrow space straight lambda subscript straight m space equals 500 space nm
straight lambda subscript straight m is the wavelength corresponding to maximum energy, so U2 > U1.

Question
CBSEENPH12040052
Wired Faculty App

A particle of mass 1 mg has the same wavelength as an electron moving with a velocity of 3 x 106 ms-1. The velocity of the particle is.

(mass of electron = 9.1 x 10-31 kg)

  • 2.7 x 10-18 ms-1

  •  9 x 10-2 ms-1

  • 3 x 10-31 ms-1

  • 2.7 x 10-21 ms-1

Solution

A.

2.7 x 10-18 ms-1

wavelength of a particle is given by
straight lambda space equals space straight h over straight p where space straight h space is space Planck apostrophe straight s space constant space and space wave space length space of space electron space is space given space by straight lambda subscript straight e space equals space straight h over straight p subscript straight e straight lambda space equals space straight lambda subscript straight e straight p space equals straight p subscript straight e mv space equals space straight m subscript straight e straight v subscript straight e straight v equals space straight m subscript straight e straight v subscript straight e Putting space the space under space given space data straight m subscript straight e space equals space 9.1 space straight x space 10 to the power of negative 31 end exponent space kg comma space straight v subscript straight e space equals space 3 space straight x space 10 to the power of 6 space straight m divided by straight s end exponent straight m space equals 1 space mg space equals space 1 space straight x space 10 to the power of negative 6 end exponent space kg straight v equals space fraction numerator 9.1 space straight x space 10 to the power of negative 31 end exponent space straight x space 3 space straight x space 10 to the power of 6 over denominator 1 space straight x space 10 to the power of negative 6 end exponent end fraction equals space 2 minus 7 space straight x space 10 to the power of negative 18 end exponent space ms to the power of negative 1 end exponent

Question
CBSEENPH12040092
Wired Faculty App

A photo-cell employs photoelectric effect to convert

  • change in the frequency of light into a change in electric voltage

  • change in the intensity of illumination into a change in photoelectric current

  • change in the intensity of illumination into a change in the work function of the photocathode

  • change in the frequency of light into a change in the electric current

Solution

B.

change in the intensity of illumination into a change in photoelectric current

In photoelectric effect when monochromatic radiations of suitable frequency fall on the photo-sensitive plate called cathode, the photoelectrons are emitted which get accelerated towards anode. These electrons flow in the outer circuit resulting in the photoelectric current.
Using the incident radiations of a fixed frequency, it is found that the photoelectric current increases linearly with the intensity of incident light as shown in figure. Hence, a photocell employs photoelectric effect to convert change in the intensity of illumination into a change in photoelectric current.

Question
CBSEENPH12039944
Wired Faculty App

A photoelectric surface is illuminated successively by monochromatic light of wavelength λ and λ/2. If the maximum kinetic energy of the emitted photoelectrons in the second case is 3 times that in the first case, the work function of the surface of the material is 

(h = planck's constant, c= speed of light)

  • hc/ 2λ

  • hc/λ

  • 2 hc/λ

  • hc/3λ

Solution

A.

hc/ 2λ

According to Einstein photoelectric equation,
E = Kmax + Φ
Where Kmax is the maximum kinetic energy of emitted electron and Φ is work function of electrons.
Kmax = E - Φ = hv - Φ
Kmax = hc over straight lambda minus ϕ
Similarly, in the second case, maximum kinetic energy of emitted electron is 3 times that in the first case, we get
3Kmax hc over straight lambda minus ϕ 
solving EQs (i) and (ii), we get work function of an emitted electron from a metal surface.
Φ = hc/2λ

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

9