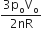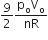Thermal Properties Of Matter
Sponsor Area
‘n’ moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be: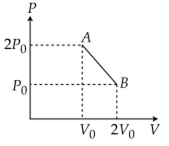
A.
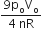
As, T will be maximum temperature where product of pV is maximum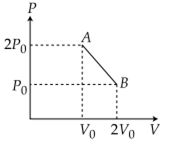
Equation of line AB, we have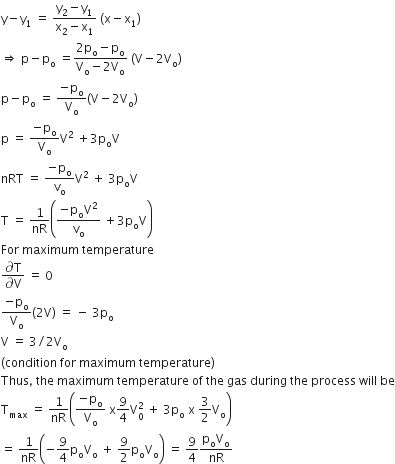
Sponsor Area
100g of water is heated from 30°C to 50°C ignoring the slight expansion of the water, the change in its internal energy is (specific heat of water is 4184 J/Kg/K)
-
8.4 kJ
-
84 kJ
-
2.1 kJ
-
4.2 kJ
A.
8.4 kJ
ΔQ = M,S,ΔT
= 100 × 10-3 × 4.184 × 20 = 8.4 × 103
ΔQ = 84 kJ, ΔW = 0
ΔQ = ΔV + ΔW
ΔV = 8.4 kJ
A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75°C. T is given by:(Given : room temperature = 30° C, specific heat of copper = 0.1 cal/gm°C
-
1250°C
-
825°C
-
800°C
-
885° C
D.
885° C
Heat given = Heat taken
(100) (0.1)(T – 75) = (100)(0.1)(45) + (170)(1)(45)
10(T – 75) = 450 + 7650 = 8100
T – 75 = 810
T = 885 °C
A heater coil is cut into two equal parts and only one part is now used in the heater. The heat generated will now be
-
doubled
-
four times
-
one fourth
-
halved
A.
doubled
A light ray is incident perpendicular to one face of a 90° prism and is totally internally reflected at the glass-air interface. If the angle of reflection is 45°, we conclude that the refractive index n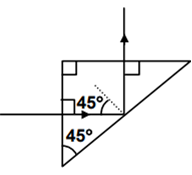
-
n<2
-

-
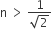
-
n<1/2
B.

Angle of incidence i > C for total internal reflection.
Here i = 45° inside the medium. ∴ 45° > sin−1 (1/n)
⇒ n > √2.
Sponsor Area
Mock Test Series
Mock Test Series