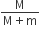A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time

• at the highest position of the platform

• at the mean position of the platform

• for an amplitude of g/ω² 

• for an amplitude of g2/ ω² 

A magnetic needle of magnetic moment 6.7 × 10^–2 Am² and moment of inertia 7.5 × 10^–6 kg m² is performing simple harmonic oscillations in a magnetic field of 0.01 T.Time taken for 10 complete oscillations is :

• 6.98 s 

• 8.76 s

• 6.65 s

• 8.89 s

A mass M, attached to a horizontal spring, executes SHM with an amplitude A₁. When the mass M passes through its mean position than a smaller mass m is placed over it and both of them move together with amplitude A₂. The ratio of (A₁/A₂) is

• 
• 
• 
• 

C.

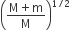
At mean position, F_net = 0
Therefore, By conservation of linear momentum,
Mv₁ = (M+m)v₂
Mω₁A₁ = (M+m)ω₂A₂
⇒ 

A particle at the end of a spring executes simple harmonic motion with a period t₁, while the corresponding period for another spring is t₂. If the period of oscillation with the two springs in series is t, then

• T = t₁ + t₂

• 
• 
• 

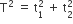
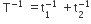
B.

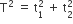
Time period of spring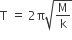

k, being the force constant of spring. For first spring and for second spring
we have,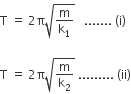

The effective force constant in their series combination is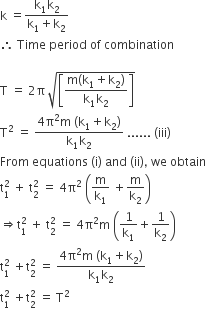

A particle is executing simple harmonic motion with a time period T. AT time t = 0, it is at its position of equilibrium. The kinetic energy-time graph of the particle will look like 

• 
• 
• 
• 

B.