Gravitation
Sponsor Area
A particle of mass 10 g is kept on the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to be done against the gravitational force between
(you may take G = 6 . 67× 10-11 Nm2/ kg2)
-
13.34 x 10-10 J
-
3.33 x 10-10 J
-
6.67 x10-9 J
-
6.67 x10-10 J
D.
6.67 x10-10 J
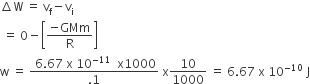
Sponsor Area
A planet in a distant solar system is 10 times more massive than the earth and its radius is 10 times smaller. Given that the escape velocity from the earth is 11 kms−1, the escape velocity from the
-
1.1 kms−1
-
11 kms−1
-
110 kms−1
-
0.11 kms−1
C.
110 kms−1
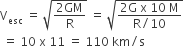
A satellite is revolving in a circular orbit at a height ‘h’ from the earth’s surface (radius of earth R ; h<<R). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth’s gravitational field, is close to: (Neglect the effect of atmosphere.)
D.

Given, a satellite is revolving in a circular orbit at a height h from the Earth's surface having radius of earth R, i.e h <<R
Orbit velocity of a satellite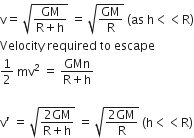
therefore, the minimum increase in its orbital velocity required to escape from the Earth's Gravitational Field.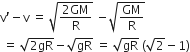
A satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
-
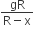
-
gx
-
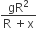
-
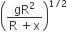
D.
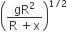
The gravitational force exerted on satellite at a height x is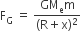
where Me = mass of earth Since, gravitational force provides the necessary centripetal force, so,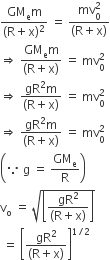
A solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same which one of the following will not be affected?
-
moment of inertia
-
angular momentum
-
angular velocity
-
rotational kinetic energy
B.
angular momentum
In free space, neither acceleration due to gravity for external torque act on the rotating solid sphere. Therefore, taking the same mass of sphere if the radius is increased then a moment of inertia, rotational kinetic energy and angular velocity will change but according to the law of conservation of momentum, angular momentum will not change.
Sponsor Area
Mock Test Series
Mock Test Series








