Atoms
Sponsor Area
As an electron makes a transition from an excited state to the ground state of a hydrogen – like atom/ion:
-
kinetic energy, potential energy and total energy decrease
-
kinetic energy decreases, potential energy increases but total energy remains same
-
kinetic energy and total energy decrease but potential energy increases
-
its kinetic energy increases but the potential energy and total energy decrease
A.
kinetic energy, potential energy and total energy decrease
As we know that kinetic energy of an electron is
KE ∝ (Z/n)2
when the electron makes the transition from an excited state of the ground state then n, decreases and KE increases. We know that PE is lowest for the ground state. As TE=- KE and TE also decreases.
Sponsor Area
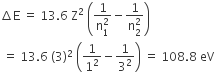
Energy required for the electron excitation in Li++ from the first to the third Bohr orbit is
-
36.3 eV
-
108.8 eV
-
122.4 eV
-
12.1 eV
B.
108.8 eV
Hydrogen (1H1), deuterium (1H2), singly ionised helium (2He4+) and doubly ionised lithium (3Li8)2+ all have one electron around the nucleus. Consider an electron transition from n =2 to n=1. If the wavelengths of emitted radiation are λ1,λ2,λ3 andλ4, respectively for four elements, then approximately which one of the following is correct?
-
4λ1=2λ2=2λ3 =λ4
-
λ1=2λ2=2λ3 =λ4
-
λ1=λ2=4λ3 =9λ4
-
λ1=2λ2=3λ3 =4λ4
C.
λ1=λ2=4λ3 =9λ4
For hydrogen atom, we get
If a source of power 4kW produces 1020 photons/second, the radiation belongs to a part of the spectrum called
-
X -rays
-
ultraviolet rays
-
microwaves
-
γ rays
A.
X -rays
As power of source = 4 x 103 = 1020 x hv
(∴ P/E = Number of photons)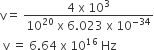
In a hydrogen like atom, electron makes the transition from an energy level with quantum number n to another with a quantum number (n – 1). If n >> 1, the frequency of radiation emitted is proportional to
-
1/n
-
1/n2
-
1/n3/2
-
1/n3
D.
1/n3
An energy gap, ΔE = hv
Here, h is Planck's constant
therefore,
Frequency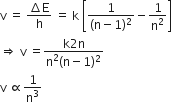
Sponsor Area
Mock Test Series
Mock Test Series





