Relations And Functions
Sponsor Area
 [cot x]dx, where [.] denotes the greatest integer function, is equal to
[cot x]dx, where [.] denotes the greatest integer function, is equal to
-
π/2
-
1
-
-1
-
– π/2
π/2
1
-1
– π/2
D.
– π/2
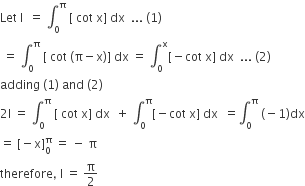
Sponsor Area
A function is matched below against an interval where it is supposed to be increasing. Which of the following pairs is incorrectly matched?
-
Interval Function (-∞, ∞) x3 – 3x2 + 3x + 3 -
Interval Function [2, ∞) 2x3 – 3x2 – 12x + 6 -
Interval Function (-∞, 1/3] 3x2 – 2x + 1 -
Interval Function (- ∞, -4] x3 + 6x2 + 6
C.
| Interval | Function |
| (-∞, 1/3] | 3x2 – 2x + 1 |
Clearly function f(x) = 3x2 – 2x + 1 is increasing when
f′(x) = 6x – 2 ≥ 0 ⇒ x∈[1/3, ∞)
A real valued function f(x) satisfies the functional equation f(x – y) = f(x) f(y) – f(a – x) f(a + y) where a is a given constant and f(0) = 1, f(2a – x) is equal to
-
–f(x)
-
f(x)
-
f(a) + f(a – x)
-
f(-x)
A.
–f(x)
f(a – (x – a)) = f(a) f(x – a) – f(0) f(x)
= - f(x) [ ∵ x = 0, y= 0, f(0) = f2 (0)-f2(a) = 0 ⇒ f(a) = 0]
Consider the following relations:
R = {(x, y)| x, y are real numbers and x = wy for some rational number w}; S = {(m/p, p/q)| m, n, p and q are integers such that n, q ≠ 0 and qm = pn}. Then
-
R is an equivalence relation but S is not an equivalence relation
-
neither R nor S is an equivalence relation
-
S is an equivalence relation but R is not an equivalence relation
-
R and S both are equivalence relations
D.
R and S both are equivalence relations
For real x, let f(x) = x3+ 5x + 1, then
-
f is one–one but not onto R
-
f is onto R but not one–one
-
f is one–one and onto R
-
f is neither one–one nor onto R
C.
f is one–one and onto R
f(x) = x3+ 5x + 1
f'(x )3x2 +5>0
⇒ f is one–one
therefore, f is cubic
⇒ f is onto
‘f’ is one–one and onto.
Sponsor Area
Mock Test Series
Mock Test Series





