Probability
Sponsor Area
A box contains 15 green and 10 yellow balls. If 10 balls are randomly drawn, one–by–one, with replacement, then the variance of the number of green balls drawn is
-
6/25
-
12/5
-
6
-
4
B.
12/5
We can apply binomial probability distribution Variance = npq
5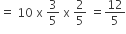
Sponsor Area
A man X has 7 friends, 4 of them are ladies and 3 are men. His wife Y also has 7 friends,3 of them are ladies and 4 are men. Assume X and Y have no common friends. Then the total number of ways in which X and Y together can throw a party inviting 3 ladies and 3 men, so that 3 friends of each of X and Y are in this party, is
-
484
-
485
-
468
-
469
B.
485
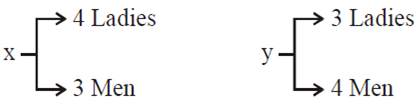
Total number of ways
4C0 · 3C3 · 3C3 · 4C0 + 4C1 · 3C2 · 3C2 · 4C1 + 4C2 · 3C1 · 3C1 · 4C2 + 4C3 · 3C0 · 3C0 · 4C3= 485
A pair of fair dice is thrown independently three times. The probability of getting a score of exactly 9 twice is
-
1/729
-
8/9
-
8/729
-
8/243
D.
8/243
Probability of getting score 9 in a single throw = 4/36 = 1/9
Probability of getting score 9 exactly twice = 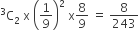
A random variable X has Poisson distribution with mean 2. Then P(X > 1.5) equals
-
2/e2
-
0
-
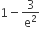
-
3/e2
C.
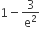
A random variable X has the probability distribution:
| X: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P(X): | 0.15 | 0.23 | 0.12 | 0.10 | 0.20 | 0.08 | 0.07 | 0.05 |
For the events E = {X is a prime number} and F = {X < 4}, the probability P (E ∪ F) is
-
0.87
-
0.77
-
0.35
-
0.50
B.
0.77
E = {x is a prime number} = {2, 3, 5, 7}
P(E) = P(X = 2) + P(X = 3) + P(X = 5) + P(X = 7)
P(E) = 0.23 + 0.12 + 0.20 + 0.07 = 0.62
F = {X < 4}= {1, 2, 3}
P(F) = P(X = 1) + P(X = 2) + P(X = 3)
P(F) = 0.15 + 0.23 + 0.12 = 0.5
E ∩ F = {X is prime number as well as < 4 }
= {2, 3}
P (E ∩ F) = P(X = 2) + P(X = 3)
= 0.23 + 0.12 = 0.35
∴ Required probability
P (E∪ F) = P(E) + P(F) - P(E ∩ F)
P (E∪ F) = 0.62 + 0.5 - 0.35
P (E ∪ F) = 0.77
Sponsor Area
Mock Test Series
Mock Test Series





