Matrices
Sponsor Area
If A and B are square matrices of size n × n such that A2 − B2 = (A − B) (A + B), then which of the following will be always true?
-
A = B
-
AB = BA
-
either of A or B is a zero matrix
-
either of A or B is an identity matrix
B.
AB = BA
A2 − B2 = (A − B) (A + B)
A2 − B2 = A2 + AB − BA − B2
⇒ AB = BA
Sponsor Area
If A2 – A + I = 0, then the inverse of A is
-
A + I
-
A
-
A – I
-
I – A
D.
I – A
Given A2 – A + I = 0
A–1A2 – A–1A + A–1 – I = A–1⋅0 (Multiplying A–1 on both sides)
⇒ A - I + A-1 = 0 or A–1 = I – A.
If a2 + b2 + c2 = -2 and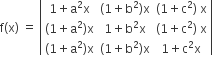 
then f(x) is a polynomial of degree
-
1
-
0
-
2
-
3
C.
2
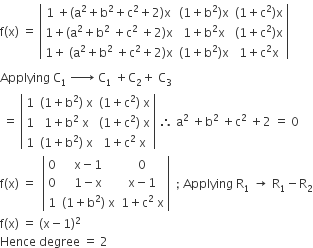
If P = 
is the adjoint of a 3 x3 matrix A and |A| = 4, then α is equal to
-
4
-
11
-
5
-
0
B.
11
Given,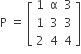 
|P| = 1(12-12)-α (4-6) +3(4-6)
= 2α -6.
∵ P =adj(A)
∴ |P| = |adj A | = |A|3-1 = |A|2 = 16
[∵ |adj A| = |A|n-1 order is 3 x3
∴ 2α -6 = 16
2α = 22
α = 11
If S is the set of distinct values of 'b' for which the following system of linear equations
x + y + z = 1
x + ay + z = 1
ax + by + z = 0
has no solution, then S is
-
a singleton
-
an empty set
-
an infinite set
-
a finite set containing two or more elements
A.
a singleton
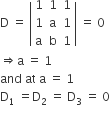
but at a = 1 and b =1
First two equations are x +y+ z =1
and third equations is x + y +z = 0
⇒ There is no solution
therefore, b = {1}
⇒ it is a singleton set
Sponsor Area
Mock Test Series
Mock Test Series