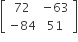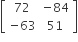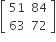+91-8076753736 support@wiredfaculty.com
Wired Faculty Logo
Wired Faculty Logo Wired Faculty

Determinants

Sponsor Area

Question
CBSEENMA12036030
Wired Faculty App

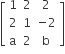A = open square brackets table row 1 2 2 row 2 1 cell negative 2 end cell row straight a 2 straight b end table close square brackets is a matrix satisfying the equation AAT = 9I, Where I is 3 x 3 identity matrix, then the ordered pair (a,b) is equal to

  • (2,-1)

  • (-2,1)

  • (2,1)

  • (-2,-1)

Solution

D.

(-2,-1)

Given, 
WiredFaculty.
It is given that,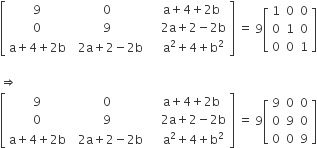
WiredFaculty
On comparing we get,
a+ 4 +2b = 0
a+ 2b = -4   ... (i)
2a + 2-2b = 0
a-b= -1    ... (ii)
a2 + 4 +b2 = 9  ... (iii)
On solving eqs. (i) and (ii) we get
a = - 2, b = - 1
Hence, (a,b) ≡ (-2,-1)

Sponsor Area

Question
CBSEENMA12036102
Wired Faculty App

Consider the system of linear equation
x1 + 2x2 + x3 = 3
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1
The system has

  • infinite number of solutions

  • exactly 3 solutions

  • a unique solution

  • no solution

Solution

D.

no solution

Subtracting the Eq. (ii) – Eq. (i)
We get x1 + x2 = 0
Subtract equations
Eq. (iii) – 2 × eq. (ii)
x1 + x2 = 5

Therefore, no solutions

Question
CBSEENMA12036009
Wired Faculty App

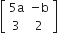If A = open square brackets table row cell 5 straight a end cell cell negative straight b end cell row 3 2 end table close square brackets and A adj A = AAT, then 5a +b is equal to

  • -1

  • 5

  • 4

  • 5

Solution

B.

5

Given, A =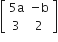open square brackets table row cell 5 straight a end cell cell negative straight b end cell row 3 2 end table close square brackets and A adj A = AAT, Clearly, A (adj A) = |A|In|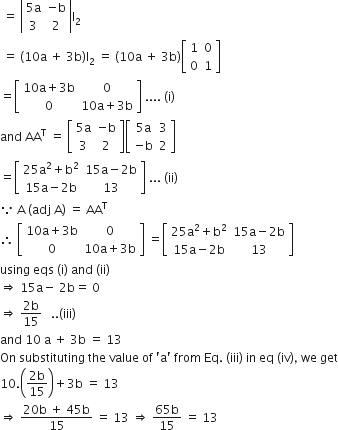
WiredFaculty
Now, substituting the value of b in Eq. (iii) we get 
5a = 2
Hence, 5a + b = 2 +3 = 5

Question
CBSEENMA12036048
Wired Faculty App

If A is a 3x3 non- singular matrix such that AAT = ATA, then BBT is equal to

  • l +B
  • l

  • B-1

  • (B-1)T

Solution

B.

l

If A is non - singular matrix then |A| ≠0
AAT = ATA and B = A-1AT
BBT = (A-1AT)(A-1AT)T
= A-1ATA(A-1)T       [∵ (AB)T= BTAT]
=A-1AAT(A-1)T        [∵ AAT = ATA]
=AT(A-1)T              [ ∵A-1A = l]
=A-1A)T                 [∵ (AB)T = BTAT]
lT = l

Question
CBSEENMA12036136
Wired Faculty App

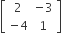If A, open square brackets table row 2 cell negative 3 end cell row cell negative 4 end cell 1 end table close square bracketsthen adj (3A2 + 12A) is equal to

  • open square brackets table row 72 cell negative 63 end cell row cell negative 84 end cell 51 end table close square brackets
  • open square brackets table row 72 cell negative 84 end cell row cell negative 63 end cell 51 end table close square brackets
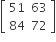
  • open square brackets table row 51 63 row 84 72 end table close square brackets
  • open square brackets table row 51 84 row 63 72 end table close square brackets

Solution

C.

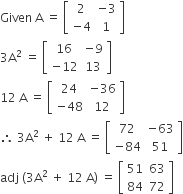
open square brackets table row 51 63 row 84 72 end table close square brackets WiredFaculty

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation