Complex Numbers And Quadratic Equations
Sponsor Area
Let α and β be the roots of equations x2-6x-2 = 0. If an =αn- βn, for n≥1, the value of a10-2a8/2a9 is equal to
-
6
-
-6
-
3
-
-3
6
-6
3
-3
C.
3
α and β are the roots of the equation
x2-6x-2 =0
or
α2 =6x+2
α2 = 6α +2
α10= 6 α9+2α8 ... (i)
β10= 6 β9+2β8 ... (ii)
On subtracting eq (ii) from eq(i), we get
α10- β10= 6 ( α9-β9) + 2 (α8 -β8)
a10 = 6a9 + 2a8 (∴ an = αn- βn)
⇒ a10 -2a8 = 6a9
⇒ a10-2a8/2a9 = 3
Sponsor Area
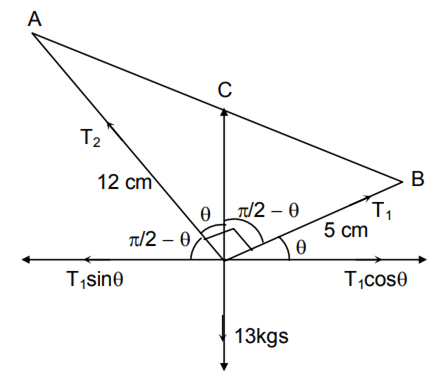
A body weighing 13 kg is suspended by two strings 5 m and 12 m long, their other ends being fastened to the extremities of a rod 13 m long. If the rod be so held that the body hangs immediately below the middle point. The tensions in the strings are
-
12 kg and 13 kg
-
5 kg and 5 kg
-
5 kg and 12 kg
-
5 kg and 13 kg
C.
5 kg and 12 kg
A complex number z is said to be unimodular, if |z|= 1. suppose z1 and z2 are complex numbers such that 
is unimodular and z2 is not unimodular. Then, the point z1 lies on a
-
straight line parallel to X -axis
-
straight line parallel to Y -axis
-
circle of radius 2
-
circle of radius
C.
circle of radius 2
If z unimodular, then |z| = 1, also, use property of modulus i.e. 
Given, z2 is not unimodular i.e |z2|≠1 and 
is unimodular
All the values of m for which both roots of the equations x2 − 2mx + m2 − 1 = 0 are greater than −2 but less than 4, lie in the interval
-
−2 < m < 0
-
m > 3
-
−1 < m < 3
-
1 < m < 4
C.
−1 < m < 3
Equation x2 − 2mx + m2 − 1 = 0
(x − m)2 − 1 = 0
(x − m + 1) (x − m − 1) = 0
x = m − 1, m + 1 − 2 < m − 1 and m + 1 < 4
m > − 1 and m < 3 − 1 < m < 3.
If (1 – p) is a root of quadratic equation x2 +px + (1-p)=0 , then its roots are
-
0, 1
-
-1, 2
-
0, -1
-
-1, 1
C.
0, -1
Since (1 - p) is the root of quadratic equation
x2 + px + (1 - p) = 0 ........ (i)
So, (1 - p) satisfied the above equation
∴ (1 - p)2 + p(1 - p) + (1 - p) = 0
(1 - p)[1 - p + p + 1] = 0 (1 - p)(2) = 0
⇒ p = 1 On putting this value of p in equation (i)
x2 + x = 0
⇒ x(x + 1) = 0 ⇒ x = 0, -1
Sponsor Area
Mock Test Series
Mock Test Series