Three Dimensional Geometry
Sponsor Area
A and B are two like parallel forces. A couple of moment H lies in the plane of A and B and is contained with them. The resultant of A and B after combining is displaced through a distance
-
2H/A-B
-
H/A+B
-
H/2(A+B)
-
H/A-B
B.
H/A+B
(A + B) = d = H
d = (H/A+B)
Sponsor Area
A line AB in three-dimensional space makes angles 45° and 120° with the positive x-axis and the positive y-axis respectively. If AB makes an acute angle θ with the positive z-axis, then θ
-
30°
-
45°
-
60°
-
75°
C.
60°
cos2α +cos2β + cos2γ = 1
α = 45°,β = 120°, γ = θ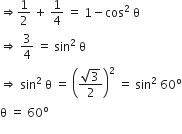
A line makes the same angle θ, with each of the x and z-axis. If the angle β, which it makes with y-axis, is such that sin2β = 3sin2θ , then cos2θ equals
-
2/3
-
1/5
-
3/5
-
2/3
C.
3/5
A line makes angle θ with x-axis and z-axis and β with y-axis.
∴ l = cosθ, m = cosβ,n = cosθ
We know that, l2+ m2+ n2= 1
cos2θ + cos2β +cos2θ =1
2cos2θ = 1- cos2β
2cos2θ = sin2β
But sin2β = 3 sin2θ
therefore from equation (i) and (ii)
3sin2θ = 2cos2θ
3(1-cos2θ) = 2cos2θ
3-3cos2θ = 2cos2θ
3 = 5cos2θ
A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of each of the point of intersection are given by
-
(3a, 3a, 3a), (a, a, a)
-
(3a, 2a, 3a), (a, a, a)
-
(3a, 2a, 3a), (a, a, 2a)
-
(2a, 3a, 3a), (2a, a, a)
B.
(3a, 2a, 3a), (a, a, a)
Any point on the line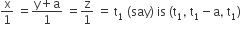 
and any point on the line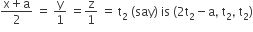 
Now direction cosine of the lines intersecting the above lines is proportional to (2t2 – a – t1, t2 – t1 + a, t2 – t1).
Hence 2t2 – a – t1 = 2k , t2 – t1 + a = k and t2 – t1 = 2k
On solving these, we get t1 = 3a , t2 = a. Hence points are (3a, 2a, 3a) and (a, a, a).
Angle between the tangents to the curve y = x2 − 5x + 6 at the points (2, 0) and (3, 0) is
-
π/2
-
π/4
-
π/6
-
π
A.
π/2
Sponsor Area
Mock Test Series
Mock Test Series