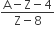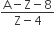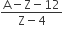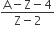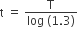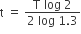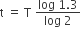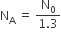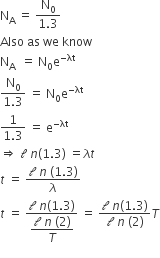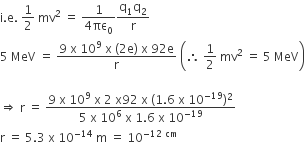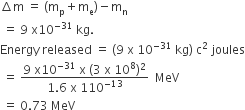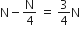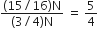Nuclei

Question

A radioactive nucleus (initial mass number A and atomic number Z) emits 3 α–particles and 2 positions. The ratio of number of neutrons to that of protons in the final nucleus will be

$fraction numerator straight A minus straight Z minus 8 over denominator straight Z minus 4 end fraction$
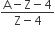
$fraction numerator straight A minus straight Z minus 4 over denominator straight Z minus 4 end fraction$
$fraction numerator straight A minus straight Z minus 12 over denominator straight Z minus 4 end fraction$
$fraction numerator straight A minus straight Z minus 4 over denominator straight Z minus 2 end fraction$

Solution

fraction numerator straight A minus straight Z minus 4 over denominator straight Z minus 4 end fraction

In positive beta decay a, proton is transformed into a neutron and a positron is emitted
p⁺ → n⁰ + e⁺
Number of neutrons initially was A-Z
Number of neutrons after decay (A-Z) -3 x 2 (due to alpha particles) + 2 x 1 (due to positive beta decay)
The number of protons will reduce by 8. so, the ratio number of neutrons to that of protons = $fraction numerator straight A minus straight Z minus 4 over denominator straight Z minus 8 end fraction$

Question

Wired Faculty App

A radioactive nucleus A with a half-life T, decays into a nucleus B. At t = 0, there is no nucleus B. At some time t, the ratio of the number of B to that of A is 0.3. Then, t is given by

t = T log (1.3)

$straight t space equals space fraction numerator straight T over denominator log space left parenthesis 1.3 right parenthesis end fraction$
$straight t space equals space fraction numerator straight T space log space 2 over denominator 2 space log space 1.3 end fraction$
$straight t space equals space straight T space fraction numerator log space 1.3 over denominator log space 2 end fraction$

Solution

straight t space equals space straight T space fraction numerator log space 1.3 over denominator log space 2 end fraction

At time t
$straight N subscript straight A space equals space fraction numerator straight N subscript 0 over denominator 1.3 end fraction$

also let initially there are total N₀ number of nuclei
N_A + N_B = N₀
$straight N subscript straight A space equals space fraction numerator straight N subscript 0 over denominator 1.3 end fraction Also space as space we space know straight N subscript straight A space space equals space straight N subscript 0 straight e to the power of negative λt end exponent fraction numerator straight N subscript 0 over denominator 1.3 end fraction space equals space straight N subscript 0 straight e to the power of negative λt end exponent fraction numerator 1 over denominator 1.3 end fraction space equals space straight e to the power of negative λt end exponent rightwards double arrow space calligraphic l space n left parenthesis 1.3 right parenthesis space equals lambda t t space equals space fraction numerator </p> </div> </div> <div class=$

Question

Wired Faculty App

An α-particle of energy 5 MeV is scattered through 180° by a fixed uranium nucleus. The distance of the closest approach is of the order of

1 Å

10⁻¹⁰ cm

10⁻¹² cm

10⁻¹⁵ cm

Solution

10⁻¹² cm

At closest approach, all the kinetic energy of the α-particle will converted into the potential energy of the system, K.E. = P.E.
$straight i. straight e. space 1 half space mv squared space equals space fraction numerator 1 over denominator 4 πε subscript 0 end fraction fraction numerator straight q subscript 1 straight q subscript 2 over denominator straight r end fraction 5 space MeV space equals space fraction numerator 9 space straight x space 10 to the power of 9 space straight x space left parenthesis 2 straight e right parenthesis space straight x space 92 straight e over denominator straight r end fraction space open parentheses therefore space 1 half space mv squared space equals space 5 space MeV close parentheses rightwards double arrow space straight r space equals space fraction numerator 9 space straight x space 10 to the power of 9 space straight x space 2 space straight x 92 space straight x space left parenthesis 1.6 space straight x space 10 to the power of negative 19 end exponent right parenthesis squared over denominator 5 space straight x space 10 to the power of 6 space straight x space 1.6 space straight x space 10 to the power of negative 19 end exponent end fraction straight r space equals space 5.3 space straight x space 10 to the power of negative 14 end exponent space straight m space equals space 10 to the power of negative 12 space cm end exponent$

Sponsor Area

Question

Wired Faculty App

Assume that a neutron breaks into a proton and an electron. The energy released during this process is(Mass of neutron = 1.6725 x 10^–27kg; mass of proton = 1.6725 x 10^–27kg; mass of electron = 9 x 10^–31kg)

0.73 MeV

7.10 MeV

6.30 MeV

5.4 MeV

Solution

0.73 MeV

increment straight m space equals space left parenthesis straight m subscript straight p plus straight m subscript straight e right parenthesis minus straight m subscript straight n space equals space 9 space straight x 10 to the power of negative 31 end exponent space kg. Energy space released space equals space left parenthesis 9 space straight x space 10 to the power of negative 31 end exponent space kg right parenthesis space straight c squared space joules space equals space fraction numerator 9 space straight x 10 to the power of negative 31 end exponent space straight x space left parenthesis 3 space straight x space 10 to the power of 8 right parenthesis squared over denominator 1.6 space straight x space 110 to the power of negative 13 end exponent end fraction space space MeV space equals space 0.73 space MeV

Sponsor Area

Question

Wired Faculty App

Half-lives of two radioactive elements A and B are 20 minutes and 40 minutes, respectively. Initially, the samples have equal number of nuclei. After 80 minutes, the ratio of decayed numbers of A and B nuclei will be:

1: 16

4 : 1

1: 4

5: 4

Solution

5: 4

Given 80 min = 4 half-lives of A = 2 half-lives of B.
Let the initial number of nuclei in each sample be N.
For radioactive element A,
N_A after 80 min = N/2⁴
⇒ Number of A nuclides decayed = $straight N minus straight N over 16 space equals space 15 over 16 straight N$

For radioactive element B,
N_B after 80 min = N/2²
⇒ Number of B nuclides decayed
=

straight N minus straight N over 4 space equals space 3 over 4 straight N

therefore, the ratio of decayed numbers of A and B nuclei will be

fraction numerator open parentheses 15 divided by 16 close parentheses straight N over denominator left parenthesis 3 divided by 4 right parenthesis straight N end fraction space equals space 5 over 4

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

Nuclei

An α-particle of energy 5 MeV is scattered through 180° by a fixed uranium nucleus. The distance of the closest approach is of the order of

1 Å

10⁻¹⁰ cm

10⁻¹² cm

10⁻¹⁵ cm

Assume that a neutron breaks into a proton and an electron. The energy released during this process is(Mass of neutron = 1.6725 x 10^–27kg; mass of proton = 1.6725 x 10^–27kg; mass of electron = 9 x 10^–31kg)

0.73 MeV

7.10 MeV

6.30 MeV

5.4 MeV

Half-lives of two radioactive elements A and B are 20 minutes and 40 minutes, respectively. Initially, the samples have equal number of nuclei. After 80 minutes, the ratio of decayed numbers of A and B nuclei will be:

1: 16

4 : 1

1: 4

5: 4

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Location

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

Nuclei

A radioactive nucleus (initial mass number A and atomic number Z) emits 3 α–particles and 2 positions. The ratio of number of neutrons to that of protons in the final nucleus will be

A radioactive nucleus A with a half-life T, decays into a nucleus B. At t = 0, there is no nucleus B. At some time t, the ratio of the number of B to that of A is 0.3. Then, t is given by t = T log (1.3)

An α-particle of energy 5 MeV is scattered through 180° by a fixed uranium nucleus. The distance of the closest approach is of the order of 1 Å 10−10 cm 10−12 cm 10−15 cm

Assume that a neutron breaks into a proton and an electron. The energy released during this process is(Mass of neutron = 1.6725 x 10–27kg; mass of proton = 1.6725 x 10–27kg; mass of electron = 9 x 10–31kg) 0.73 MeV 7.10 MeV 6.30 MeV 5.4 MeV

Half-lives of two radioactive elements A and B are 20 minutes and 40 minutes, respectively. Initially, the samples have equal number of nuclei. After 80 minutes, the ratio of decayed numbers of A and B nuclei will be: 1: 16 4 : 1 1: 4 5: 4

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

An α-particle of energy 5 MeV is scattered through 180° by a fixed uranium nucleus. The distance of the closest approach is of the order of

1 Å

10⁻¹⁰ cm

10⁻¹² cm

10⁻¹⁵ cm

Assume that a neutron breaks into a proton and an electron. The energy released during this process is(Mass of neutron = 1.6725 x 10^–27kg; mass of proton = 1.6725 x 10^–27kg; mass of electron = 9 x 10^–31kg)

0.73 MeV

7.10 MeV

6.30 MeV

5.4 MeV

Half-lives of two radioactive elements A and B are 20 minutes and 40 minutes, respectively. Initially, the samples have equal number of nuclei. After 80 minutes, the ratio of decayed numbers of A and B nuclei will be:

1: 16

4 : 1

1: 4

5: 4