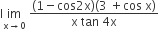 is equal to
is equal to
-
4
-
3
-
2
-
1/2
4
3
2
1/2
C.
2
We have,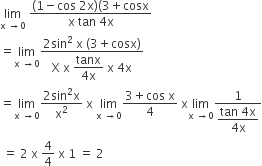
Sponsor Area
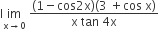 is equal to
is equal to
4
3
2
1/2
C.
2
We have,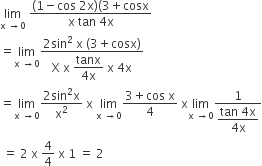
Sponsor Area
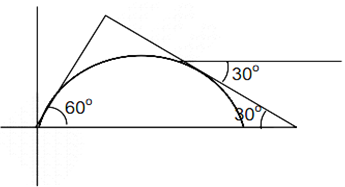
A particle is projected from a point O with velocity u at an angle of 60o with the horizontal. When it is moving in a direction at right angles to its direction at O, its velocity then is given by
u/3
u/2
2u/3
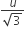
D.
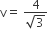
A value of θ for which 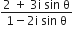 is purely imaginary is
is purely imaginary is
π/3
π/6
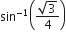
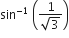
D.
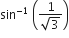
Let z = 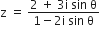 is purely imaginary. Then, we have Re (z) = 0
is purely imaginary. Then, we have Re (z) = 0
We have Re (z) = 0
Now, consider z = 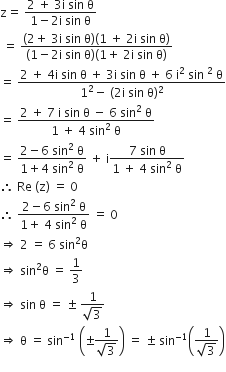
Consider f(x) = tan-1 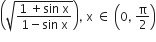 . A normal to y = f (x) at x = π/6 also passes through the point
. A normal to y = f (x) at x = π/6 also passes through the point
(0,0)
(0, 2π/3)
(π/6 ,0)
(π/4, 0)
B.
(0, 2π/3)
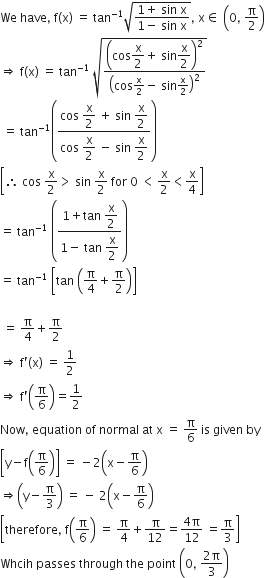
If 0≤x<2π, then the number of real values of x, which satisfy the equation cosx+cos2x+cos3x+cos4x=0, is :
3
5
7
9
C.
7
Sponsor Area
Mock Test Series