Ratio And Proportion
Sponsor Area
80 is divided into three parts, such that the first part is 24 and the ratio of the second to the third is 4 : 3. The second part is
-
40
-
36
-
32
-
24
C.
32
Total = 80
First part = 24
∴ Sum of second and third part = 80 - 24 = 56
Ratio of second to the third part = 4 : 3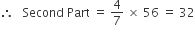
Sponsor Area
A and B earn in the ratio 2 : 1. They spend in the ratio 5 :3 and save in the ratio 4 : 1. If the total monthly savings of both A and B are ₹ 5,000 the monthly income of B is
-
₹ 7,000
-
₹ 14,000
-
₹ 5,000
-
₹ 10,000
A.
₹ 7,000
A : B (Savings ratio) = 4 : 1
Total savings = ₹ 5000
∴ A's savings = ₹ 4000
B's savings = ₹ 1000
Now according to question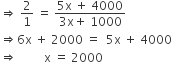
∴ B's income = 1000 + 3 x 2000 = ₹ 7000
A and B have their monthly incomes in the ratio 8 : 5, while their monthly expenditures are in the ratio 5 : 3. If they have saved Rs. 12,000 and Rs 10,000 monthly respectively, then the difference in their monthly incomes is
-
Rs 52,000
-
Rs. 42,000
-
Rs. 44,000
-
Rs. 46,000
B.
Rs. 42,000
Let A's monthly income be Rs. 8x
A's monthly expenditure be Rs. 5y
Let B's monthly income be Rs. 5x
B's monthly expenditure be Rs. 3y
According to the question,
8x - 5y = 12000 ...(i)
5x - 3y = 10000 ...(ii)
Solving (i) and (ii), we get
⟹ x = 14000
Difference between monthly incomes of A and B
= 8x - 5x = Rs. 3x = Rs. (3 x 14000)
= Rs. 42000
A bag contains Rs. 145 in the form of one-rupee, 50-paise and 25-paise coins in the ratio 3 : 5 : 7. The number of one-rupee coins is
-
60
-
50
-
48
-
45
A.
60
Ratio of the values of coins
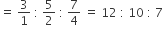
∴ Value of the one rupees coins
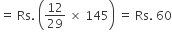
Rs.60 = Number of one rupee coins
A certain amount of money is divided between A and B in the ratio of 5:6. If B gets ₹360/-, the amount is
-
₹660/-
-
₹560/-
-
₹680/-
-
₹580/-
A.
₹660/-
Let the amount = ₹ x
According to the question,
Share of B = 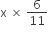
360 = 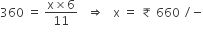
Sponsor Area
Mock Test Series
Mock Test Series





