Coordinate Geometry
Sponsor Area
Area of the triangle formed by the graph of the straight lines x - y = 0, x + y = 2 and x-axis is
-
1 sq unit
-
2 sq units
-
1 sq units
-
None of these
A.
1 sq unit
On putting x = 0 in
x + y = 2,
0 + y = 2 ⟹ y = 2
∴ Point of intersection on y-axis (0, 2)
Again, putting y = 0 in x + y = 2, ⟹ x = 2
∴ Point of intersection on x-axis = (2, 0)
x - y = 0 will pass through origin and be equally inclined to axes.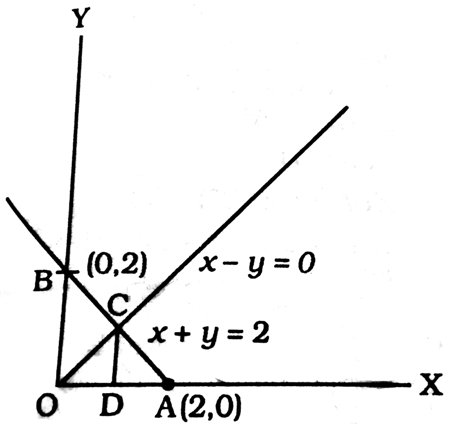
On putting x = y in x + y = 2,
2y = 2 ⟹ y = 1
∴ CD = 1
OA = 2
Area of ΔOAC = 
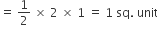
Sponsor Area
If the ordinate and abscissa of the point (k, 2k -1) be equal, then the value of k is
-
0
-
-1
-
1
-
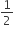
C.
1
Abscissa = k,
ordinate = 2k - 1
According to the question,
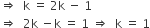
The area (in square units) of the triangle formed by the graphs of the equations x = 4, y = 3 and 3x + 4y = 12 is
-
24
-
12
-
6
-
3
C.
6
On putting x = 0 in the equation 3x + 4y = 12,
4y = 12, ⟹ y = 3
Again on putting y = 0,
3x = 12 ⟹ x = 4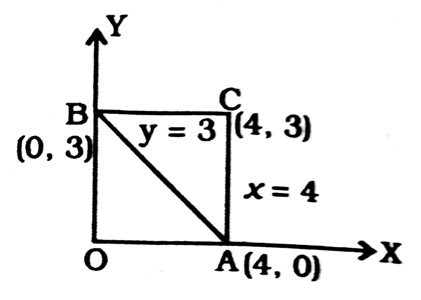
∴ Area of ΔABC = 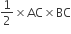
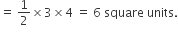
The area of the triangle formed by the graphs of the equations x = 4, y = 3 and 3x + 4y = 12 is
-
4 sq units
-
12 sq units
-
6 sq units
-
3 sq units
C.
6 sq units
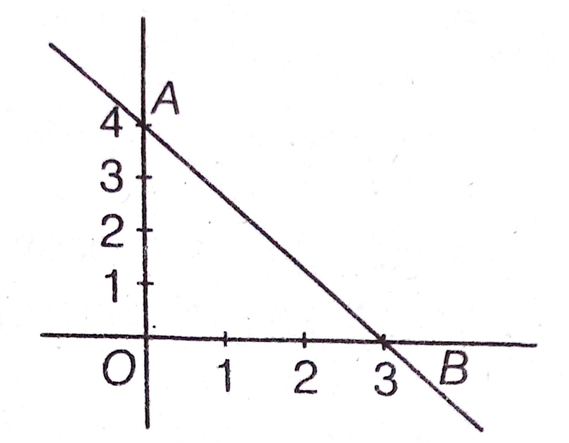
 Required area of AOB =
Required area of AOB = 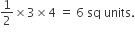
The area of the triangle formed by the straight line 3x + 2y = 6 and the co-ordinate axes is
-
3 square units
-
6 square units
-
4 square units
-
8 square units
A.
3 square units
Putting y = 0 in the equation 3x + 2y = 6
3x + 0 = 6 ⟹ x = 2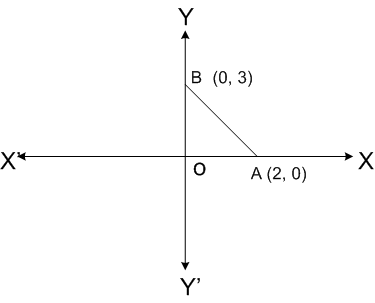
∴ Point of intersection on x-axis = (2, 0)
Putting x = 0, in the equation
3x + 2y = 6
0 + 2y = 6
⟹ y = 3
∴ Point of intersection on y-axis = (0, 3)
∴ OA = 2, OB = 3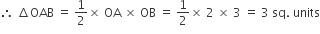
Sponsor Area
Mock Test Series
Mock Test Series





